
15ー1ー01.ステップ関数(RLC回路)
このページからは,いよいよRLC回路のステップ関数の場合の応答を調べていきます.
次は,抵抗,コイル,コンデンサが直列の回路について

入力はステップ関数となるので,
\(\Large V(t) \ : \ V_0 \ ( 0 \leq t \leq t_0) \)
\(\Large \hspace{35 pt} : \ 0 \ (0>t, t_0 < t) \)
となります.
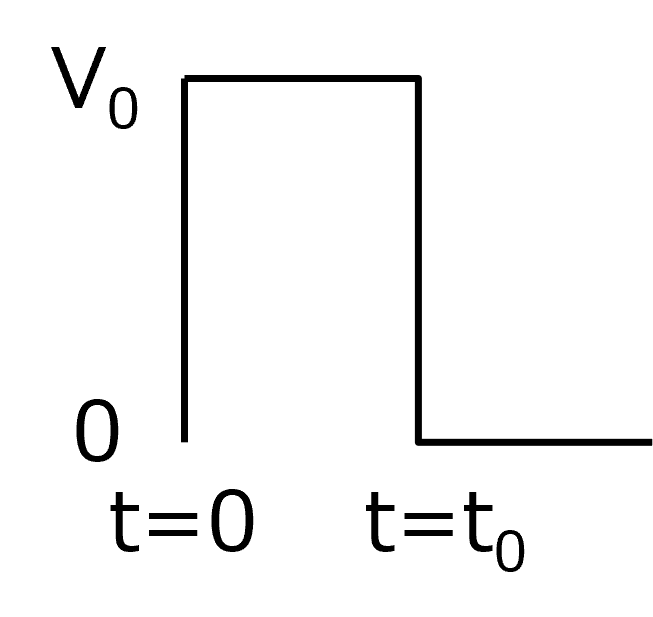
思った以上に複雑になったので,順を追って説明していきます.
2.0 < t < t0,でのステップ応答
4.コンデンサ,コイルの電圧はどうなるか
5.初期条件が,I'(0) = 0,の場合
となります.
直列なので,
電流はどこも同じ
電圧は,抵抗+コンデンサ,が電源と等しい
ことから,
\(\Large V_0 = V_R (t) + V_C (t) \)
\(\Large V_R(t) = R \cdot I(t) \)
\(\Large \displaystyle V_L(t) = L \ \frac{d}{dt} I(t) \)
\(\Large \displaystyle V_C(t) = \frac{1}{C} \ \int I(t) \ dt \)
\(\Large \displaystyle V_0 = R \cdot I(t) + L \ \frac{d}{dt} I(t) \)
\(\Large \displaystyle \frac{d}{dt} I (t) = - \frac{R}{L} I (t) + \frac{1}{L} \ V_0 \)
なる,微分方程式を解けばいいことになります.