Barkai-Leiblerモデルを考える-04

刺激直後の反応は？

メチル化がX濃度に依存する場合，を考えていきます．

刺激直後にどの程度，X_m^*，が変化するのでしょう？

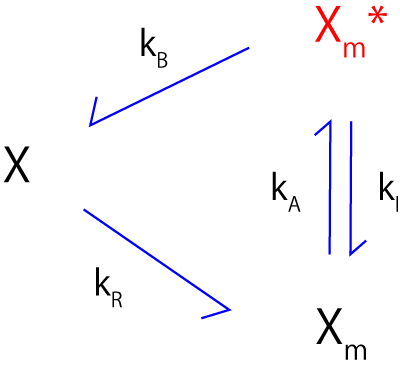
前々ページと同様に，以下のモデル図を考えます．

ここで，

X：レセプター（不活性，非メチル化）
Xm：レセプター（不活性，メチル化）
Xm*：レセプター（活性，メチル化）

となります．

刺激直後には，X_m^*，の濃度が下がり，徐々に復活し，元に戻るわけですから，

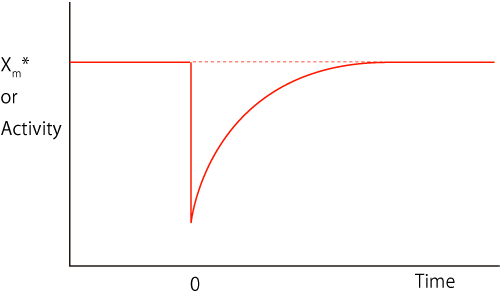
とような反応になります．

ここで，各反応速度には，

\(\Large \displaystyle k_B, k_R << k_A, k_I \)

となります，適応現象は刺激応答に対してとても遅いことからです

したがって，刺激直後の短期間の反応は，

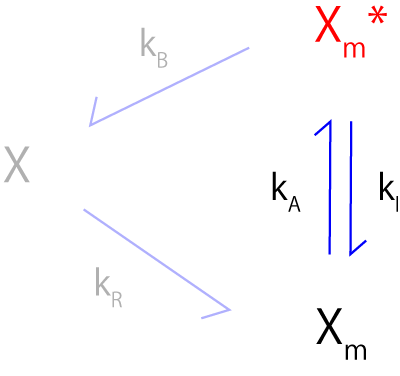
だけを考えればいいので，

\(\Large \displaystyle k_I \cdot X_m^* \vert_{t \leqq 0} = k_A \cdot X_m \vert_{t \leqq 0} \)

の関係になります（短時間には）

刺激前の，メチル化レセプターの各濃度は，ここ，に示したように(k_I=0なので），

\(\Large \displaystyle X_m^* \vert_{t \leqq 0} = \frac{ k_R \cdot R}{k_B \cdot B} \)

\(\Large \displaystyle X_m \vert_{t \leqq 0} = \frac{ k_B \cdot B +0}{k_A} \frac{ k_R \cdot R}{k_B \cdot B} = \frac{k_R \cdot R}{k_A} \)

となりますので，刺激前のメチル化レセプター全濃度は，

\(\Large \displaystyle \left( X_m^* + X_m \right) \vert_{t \leqq 0} = \frac{ k_R \cdot R}{k_B \cdot B} + \frac{k_R \cdot R}{k_A} = k_R \cdot R \left( \frac{1}{k_A} + \frac{ 1}{k_B \cdot B} \right) \)

となります．したがって，

\(\Large \displaystyle X_m \vert_{t \leqq 0} = \frac{k_I}{k_A} X_m^* \vert_{t \leqq 0} \)

\(\Large \displaystyle X_m^* \vert_{t \leqq 0} \left( 1 + \frac{k_I}{k_A} \right) = k_R \cdot R \left( \frac{1}{k_A} + \frac{ 1}{k_B \cdot B} \right) \)

\(\Large \displaystyle X_m^* \vert_{t \leqq 0} \frac{k_A + k_I}{k_A} = k_R \cdot R \frac{k_A + k_B \cdot B}{k_A \cdot k_B \cdot B} \)

\(\Large \displaystyle  \begin{eqnarray} X_m^* \vert_{t \leqq 0} &=& k_R \cdot R \frac{k_A + k_B \cdot B}{k_A \cdot k_B \cdot B} \frac{k_A }{k_A+ k_I} \\
&=& \frac{k_R \cdot R}{k_B \cdot B} \frac{k_A + k_B \cdot B}{k_A+ k_I} \\
\end{eqnarray} \)

となる（はず）です．．．．