Barkai-Leiblerモデルを考える-05

差分法

実際の反応を差分法で考えていきましょう．

各状態の時間変化は，

\(\Large \displaystyle \frac{d X_m^*}{dt} = -(k_B \cdot B + k_I \cdot I)X_m^* +k_A \cdot X_m \)

\(\Large \displaystyle \frac{d X_m}{dt} = k_I \cdot I \cdot X_m^* - k_A \cdot X_m + k_R \cdot R \)

\(\Large \displaystyle \frac{d X}{dt} = k_B \cdot B \cdot X_m^* - k_R \cdot R \)

ここで，
B：CheB濃度
R：CheR濃度
I：誘引物質
です．

つまり，誘因刺激前は，

\(\Large \ k_I \cdot I = 0 \)

刺激後は，

\(\Large \ k_I \cdot I = \ k_I \cdot I \)

となります．差分法の式は，

\(\Large \displaystyle X_m^*(t+ \Delta t) = X_m^*(t) + \Delta t [ -(k_B \cdot B + k_I \cdot I)X_m^*(t) +k_A \cdot X_m(t) ]\)

\(\Large \displaystyle X_m(t+ \Delta t) =X_m(t)+ \Delta t [k_I \cdot I \cdot X_m^* - k_A \cdot X_m + k_R \cdot R ]\)

\(\Large \displaystyle X(t+ \Delta t) = X(t) + \Delta t [k_B \cdot B \cdot X_m^* - k_R \cdot R] \)

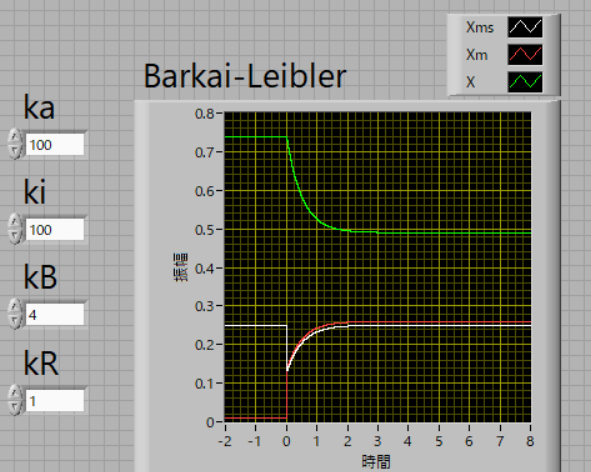
を計算していきます．その結果は，

となり，うまく説明できていることがわかります．

定常状態での各状態の濃度は，

\(\Large \displaystyle X_m^* = \frac{ k_R \cdot R}{k_B \cdot B} \)

\(\Large \displaystyle X_m = \frac{ k_B \cdot B + k_I \cdot I}{k_A} X_m^* = \frac{ k_B \cdot B + k_I}{k_A} \frac{ k_R \cdot R}{k_B \cdot B} \)

\(\Large \displaystyle X = \frac{ k_A \cdot k_B \cdot B - k_A \cdot k_R \cdot R - k_B \cdot B \cdot k_R \cdot R - k_R \cdot R \cdot k_I}{k_A \cdot k_B \cdot B} \)

であり，上図の条件では，

\(\Large \displaystyle X_m^* = \frac{ k_R \cdot R}{k_B \cdot B}= \frac{ 1}{4} = 0.25 \)

とうまく再現できています．

刺激直後においては，

\(\Large \displaystyle   X_m^* \vert_{t \leqq 0}= \frac{k_R \cdot R}{k_B \cdot B} \frac{k_A + k_B \cdot B}{k_A+ k_I} = \frac{1}{4} \frac{100+4}{100+100} = 0.13 \)

となるはずです．実際のトレースでは，0.131213，でしたので，まあまあいい感じでしょう．

バラメータを変えた場合でも（k_Bを4から2へ）

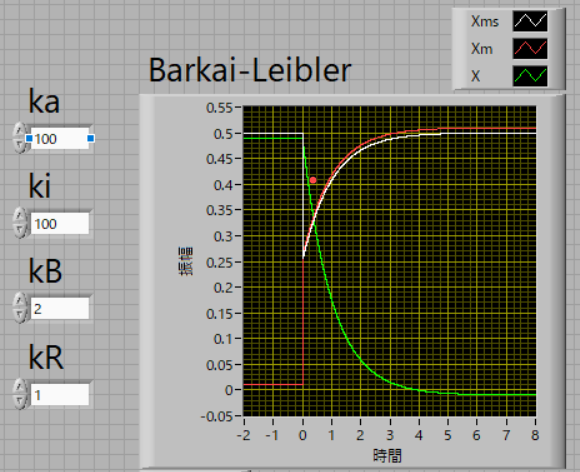
\(\Large \displaystyle   X_m^* \vert_{t \leqq 0}= \frac{k_R \cdot R}{k_B \cdot B} \frac{k_A + k_B \cdot B}{k_A+ k_I} = \frac{1}{2} \frac{100+2}{100+100} = 0.255 \)

となるはずです．実際のトレースでは，0.25706，でしたので，まあまあいい感じでしょう．

立ち上がりは，Alonの初版と同様に上凸のカーブとなりました，指数関数で近似できそうです．

では，このカーブ，各速度定数とどのような関係にあるのでしょうか？