全変動 = 回帰変動 + 残差変動の証明

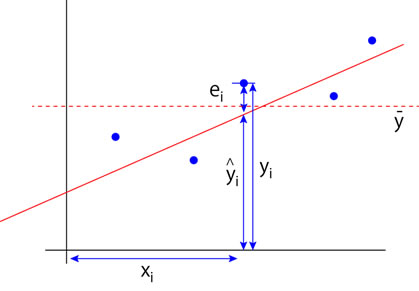
再び，同じグラフを表示します．

yiのばらつき加減は，yiの
　全体のばらつき　＝　平均値からのばらつき　＋　回帰直線からのばらつき

一般的には，

　全変動 = 回帰変動 + 残差変動

の和になると考えましょう．その証明を考えていきましょう．あくまで直線近似の場合です．

全変動　：　\( \Large \displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2 \)

回帰変動　：　\( \Large \displaystyle \sum_{i=1}^n (f(x_i) - \overline{y})^2 \)

残差変動　：　\( \Large \displaystyle \sum_{i=1}^n (y_i - f(x_i))^2 \)

となるので，

全変動ー回帰変動ー残差変動は，

\( \Large \displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2 -\sum_{i=1}^n (f(x_i) - \overline{y})^2 - \sum_{i=1}^n (y_i - f(x_i))^2 \)

\( \Large \displaystyle = \sum_{i=1}^n \left( \color{red}{y_i^2} -2 y_i \overline{y} + \color{blue}{\overline{y}^2} - f(x_i)^2 + 2 f(x_i) \overline{y} \color{blue}{- \overline{y}^2} \color{red}{- y_i^2} + 2y_i f(x_i))^2 - f(x_i)^2 \right) \)

と色つきの部分が消えますので，

\( \Large \displaystyle = \sum_{i=1}^n \left( -2 y_i \overline{y} - f(x_i)^2 + 2 f(x_i) \overline{y} + 2y_i f(x_i))^2 - f(x_i)^2 \right) \)

となります．並び替えると，

\( \Large \displaystyle = -2 \sum_{i=1}^n \left( f(x_i)^2 - f(x_i) \overline{y} - y_i f(x_i)^2 + y_i \overline{y} \right) \)

\( \Large \displaystyle = -2 \sum_{i=1}^n \left\{ f(x_i) - \overline{y} \right\} \left\{ f(x_i) - y_i \right\} \)

\( \Large \displaystyle = 2 \sum_{i=1}^n \left\{ f(x_i) - \overline{y} \right\} \left\{ y_i - f(x_i) \right\} \)

となります．ここで，

\( \Large f(x_i) = ax_i + b \)

なので，

\( \Large \displaystyle = 2 \sum_{i=1}^n \left\{ ax_i + b - \overline{y} \right\} \left\{ y_i - ax_i - b \right\} \)

となります．

切片，b，は，ここ，より，

\( \Large \displaystyle b = \overline{y} - a \overline{x} \)

ですので，

\( \Large \displaystyle 2 \sum_{i=1}^n \left\{ ax_i + b - \overline{y} \right\} \left\{ y_i - ax_i - b \right\} \)

\( \Large \displaystyle = 2 \sum_{i=1}^n \left\{ ax_i - a \overline{x} \right\} \left\{ y_i - ax_i - \overline{y} + a \overline{x} \right\} \)

\( \Large \displaystyle = 2 \sum_{i=1}^n \left\{a ( x_i - \overline{x} ) ( y_i - \overline{y} )- a^2 ( x_i - \overline{x}) ( x_i - \overline{x}) \right\} \)

\( \Large \displaystyle = 2 na \cdot Cov(X,Y) - 2n a^2 \sigma_X^2 \)

\( \Large \displaystyle = 2 na \left( Cov(X,Y) - a \cdot \sigma_X^2 \right) \)

共分散，Cov，を使いました．

傾き，a，は，ここ，より，

\( \Large \displaystyle a =\frac{ Cov(X,Y) }{ \sigma_X^2} \)

なので，括弧の中は0となります．従って，

\( \Large \displaystyle = 2 na \left( Cov(X,Y) - Cov(X,Y) \right) = 0 \)

となります．つまり，

全変動ー回帰変動ー残差変動

or

全変動=回帰変動+残差変動

となります．

次に，共分散からの決定係数の見積もりを考えましょう．