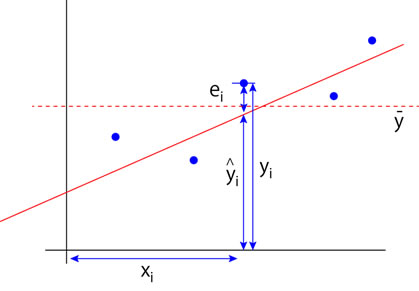
全体のばらつきからの決定係数の求め方

再び，同じグラフを表示します．

yiのばらつき加減は，yiの
　全体のばらつき　＝　平均値からのばらつき　＋　回帰直線からのばらつき

一般的には，

　全変動 = 回帰変動 + 残差変動

の和になると考えましょう．その証明は，ここ，で．
なので，
　（平均値からのばらつき）/（全体のばらつき）＝１－（回帰直線からのばらつき）/（全体のばらつき）
が1に近づくほど回帰直線によく一致することとなります．

全体のばらつきは， 各データから平均値を引いたものとなりますので，

\( \Large \displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2 \)

となります．従って，

\( \Large \displaystyle =\sum_{i=1}^n (\hat{y_i} + e_i - \overline{y} )^2 \)

\( \Large \displaystyle =\sum_{i=1}^n \{(\hat{y_i} - \overline{y}) + e_i \}^2 \)

\( \Large \displaystyle =\sum_{i=1}^n \{(\hat{y_i} - \overline{y})^2 +2 e_i (\hat{y_i} - \overline{y}) + e_i^2 \} \)

となります．
ここで，第二項は０となります（計算は，ここ，をごらんください）．
従って，

\( \Large \displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2 =\sum_{i=1}^n (\hat{y_i} - \overline{y})^2 + \displaystyle \sum_{i=1}^n e_i^2 \)

となり，

　左辺：全体のばらつき（全変動）
　右辺第一項：平均値からのばらつき　（回帰変動）
　右辺第二項：回帰直線からのばらつき　（残差変動）
となります．

従って，

\( \Large \begin{eqnarray} R^2 &=& \frac{\displaystyle \sum_{i=1}^n (\hat{y_i} - \overline{y})^2 }{\displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2} \\
&=& 1 - \frac{ \displaystyle \sum_{i=1}^n e_i^2 }{\displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2} \\
\end{eqnarray} \)

を求めることができます．

ここで，回帰直線からのばらつき　（残差変動）は，
　回帰直線と実際の値との差
となります，回帰直線を，

\( \Large f_i = f(x_i) = a x_i + b \)

と書き表すと，

\( \Large R^2 = 1 - \frac{ \displaystyle \sum_{i=1}^n (y_i - f_i)^2 }{\displaystyle \sum_{i=1}^n (y_i - \overline{y} )^2} \)

となります．

次に，共分散からの決定係数の見積もりを考えましょう．