回折-33
ナイフエッジからの回折-33
さて,ナイフエッジ後方の振幅は,前ページで示したように,以下のようになります.
\(\Large \begin{eqnarray} u(x)
&=& \int_{0}^{\infty} \frac{u_0}{z} e^{i ( \omega t - k (R + \frac{1}{2} \frac{(X-x)^2}{R} )} dx \\
& \fallingdotseq & \int_{0}^{\infty} e^{\frac{i \pi}{\lambda R} (X-x)^2} dx \\
\end{eqnarray} \)
\(\Large u(x)= \int_{0}^{\infty} e^{\frac{i \pi}{\lambda R} (X-x)^2} dx \)
となります.
ここで,
\(\Large \alpha= \sqrt{\frac{2}{\lambda R}} (X-x) \)
とおくと,
\(\Large d \ \alpha= - \sqrt{\frac{2}{\lambda R}} \ dx \)
\(\Large\hspace{ 36pt } 0 \hspace{ 4pt } \rightarrow \hspace{ 6pt } x \rightarrow \infty \\
\Large \sqrt{\frac{2}{\lambda R}} X \rightarrow \hspace{ 4pt } \alpha \hspace{ 5pt }\rightarrow -\infty \)
となりますので,
\(\Large \begin{eqnarray} u(x)
&=& \sqrt{\frac{\lambda R}{2}} \displaystyle \int_{\sqrt{\frac{2}{\lambda R}} X}^{-\infty} e^{\frac{i \pi \ \alpha^2}{2}} d \alpha \\
&=& \sqrt{\frac{\lambda R}{2}} \displaystyle \int_{\sqrt{\frac{2}{\lambda R}} X}^{-\infty} \left[ \cos \left( \frac{ \pi \ \alpha^2}{2} \right) + i \sin \left( \frac{ \pi \ \alpha^2}{2} \right) \right] \\
\end{eqnarray} \)
となります.
ここで,フレネル積分,を導入していきましょう.
\(\Large C( \alpha ) = \displaystyle \int_{0}^{\alpha} \cos \left( \frac{ \pi \ \alpha^2}{2} \right) d \alpha \\
\Large S( \alpha ) = \displaystyle \int_{0}^{\alpha} \sin \left( \frac{ \pi \ \alpha^2}{2} \right) d \alpha \)
ここで,
\(\Large C(0) = S(0) =0 \)
\(\Large C( \pm \infty) = S(\pm \infty) =\pm \frac{1}{2} \)
です.
\(\Large C(0) = S(0) =0 \)
はいいですね.積分の中が0なのでその積分の値も0です.
問題は,
\(\Large C( \pm \infty) = S(\pm \infty) =\pm \frac{1}{2} \)
これは複素積分を用いて解くことができるようです(ここ,ここ)
しかしながら,このサイト,ではガウス積分を用いて解いていました.
このサイトを参考に解いてみました.
です.
その結果,
\(\Large C( \pm \infty) = S(\pm \infty) =\pm \frac{1}{2} \)
となりました.
また,積分範囲ですが,
\(\Large \displaystyle \int_{a}^{b} = \displaystyle \int_{0}^{b} - \displaystyle \int_{0}^{a} \)
となりますので,
\(\Large \displaystyle \int_{\sqrt{\frac{2}{\lambda R}} X}^{-\infty} = \displaystyle \int_{0}^{-\infty} - \displaystyle \int_{0}^{\sqrt{\frac{2}{\lambda R}} X} \)
と分割することができます.
従って,定数項を無視して,
\(\Large \begin{eqnarray} u(x)
&=& \sqrt{\frac{\lambda R}{2}} \displaystyle \int_{\sqrt{\frac{2}{\lambda R}} X}^{-\infty} \left[ \cos \left( \frac{ \pi \ \alpha^2}{2} \right) + i \sin \left( \frac{ \pi \ \alpha^2}{2} \right) \right] d \alpha \\
&=& \displaystyle \int_{0}^{-\infty} \left[ \cos \left( \frac{ \pi \ \alpha^2}{2} \right) + i \sin \left( \frac{ \pi \ \alpha^2}{2} \right) \right] d \alpha - \displaystyle \int_{0}^{\sqrt{\frac{2}{\lambda R}} X} \left[ \cos \left( \frac{ \pi \ \alpha^2}{2} \right) + i \sin \left( \frac{ \pi \ \alpha^2}{2} \right) \right] d \alpha \\
&=& - \frac{1}{2} - i \ \frac{1}{2} - C \left( \sqrt{ \frac{2}{ \lambda R}} X \right)- i \ S \left( \sqrt{ \frac{2}{ \lambda R}} X \right) \\
&=& \left[ - \frac{1}{2} - C \left( \sqrt{ \frac{2}{ \lambda R}} X \right) \right] +i \left[ - \frac{1}{2} - S \left( \sqrt{ \frac{2}{ \lambda R}} X \right) \right] \\
\end{eqnarray} \)
となります.
強度は振幅の二乗となるので,
\(\Large \begin{eqnarray} I(X)
&=& | u(x) |^2
&=& \left[ C \left( \sqrt{ \frac{2}{ \lambda R}} X \right) + \frac{1}{2} \right] ^2 +i \left[ S \left( \sqrt{ \frac{2}{ \lambda R}} X \right) + \frac{1}{2} \right]^2 \\
\end{eqnarray} \)
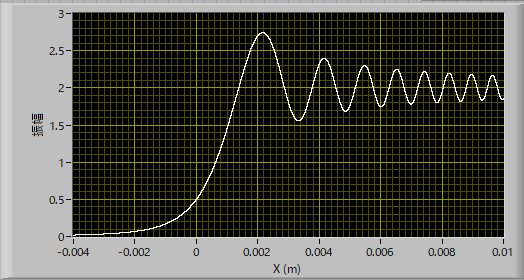
となります.実際の波形は,

となります.
これはあくまで近似式であって,
\(\Large R >>x, X \)
の場合のみに成り立つ関係式ですね.
Rをどんどん小さくしていくとどう変化していくか興味ありますね.
次ページに計算した結果をお示しします.