回折-32
ナイフエッジからの回折-32
次に,ナイフエッジからの回折を計算してみましょう.
この計算は,
光学入門
の本を参考にしました.また,フレネル積分については,
高校数学の美しい物語
フレネル積分の計算
などを参考にしました,ありがとうございます.
一般論
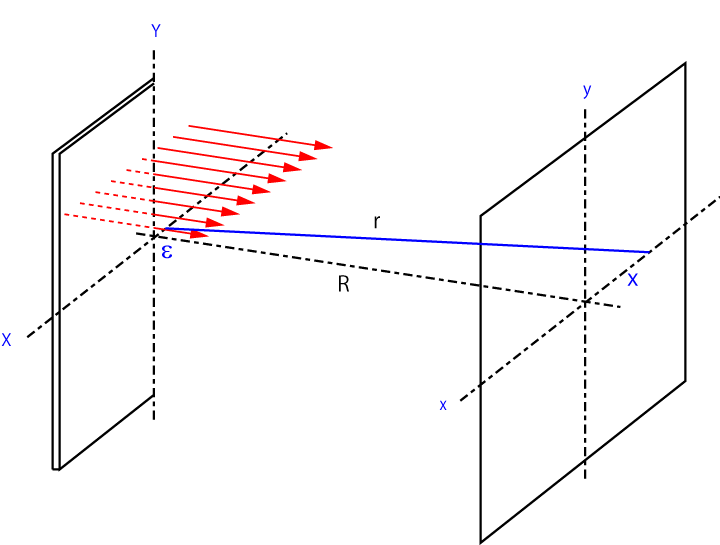
まずは,適当な形状を通過する光を考えましょう.

XY平面に任意の形状の穴を設定します.距離Rだけ離れた投影面の任意の座標(x,y)の光強度を求めます.
今回はxのみの一次元で考えます.
と同様に考えます(一次元であり,文字が少し変わってきます)
光の振動数を,ω,とすれば,その波形は,
\(\Large \sin ( \omega t - phase ) \)
となります.
位相 = 光路÷波長×2π
となるので,
\(\Large phase = \frac{r}{\lambda} \times 2 \pi = k r \)
となります.ここで,k,は波数です.従って,
\(\Large \sin ( \omega t - phase ) = \sin ( \omega t - k r ) \)
となります.光強度をE0,とすると,投影面での強度は距離zに反比例しますので,任意の開口の一部のエリアdSからの発せられる光は,
\(\Large dE = \frac{E_0}{z} \sin ( \omega t - k r ) ds \)
となります.指数表示に変換すると,
\(\Large dE = \frac{E_0}{z} e^{i ( \omega t - k r )} ds \)
となります.
次に,開口の(X, Y)から投影面(x,y)の2点間の距離を求めましょう.ここから少し変わってきます.距離rは,
\(\Large r = \sqrt{ (X-x)^2 + R^2} \)
となります.少し書き換えて,
\(\Large r = R \ \sqrt{ 1 + \frac{(X-x)^2}{R^2}} \)
となります.これを展開すると,
\(\Large r = R + \frac{1}{2} \frac{(X-x)^2}{R} \)
と簡単にできます.したがって,開口部で一元で積分すると,
\(\Large \begin{eqnarray} u(x)
&=& \int_{0}^{\infty} \frac{u_0}{z} e^{i ( \omega t - k (R + \frac{1}{2} \frac{(X-x)^2}{R} )} dx \\
& \fallingdotseq & \int_{0}^{\infty} e^{\frac{i \pi}{\lambda R} (X-x)^2} dx \\
\end{eqnarray} \)
となります.下の式への移行は,
定数項を無視した
波数を波長に戻した
です.
次ページにフレネル積分を導入していきましょう.