逐次反応における自己相関関数について-01
逐次反応

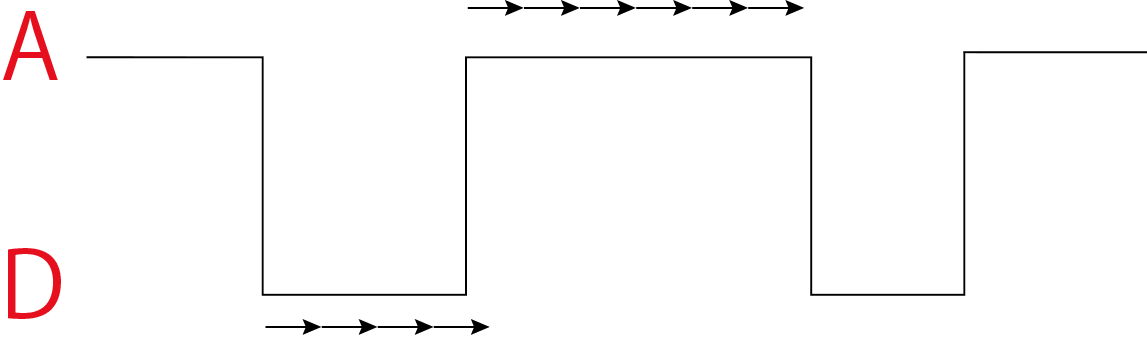
図のように,A状態(値a)とD状態(値d)をランダムに遷移する過程を考えていきましょう.
この過程では,A状態からD状態に遷移する(or D状態からA状態に遷移する)過程において単純な一次反応ではなく,複数の過程がある場合を考えます.
このときの反応式は,
\(\hspace{ 30pt } k \hspace{ 42pt } k \hspace{ 44pt } k \\[-5 pt] \Large A_0 \longrightarrow A_1 \longrightarrow \cdots \longrightarrow A_n \)
と表すことができます. この関数,f(t)の自己相関関数,<f(t)f(t+τ)>,がどのようになるかを考えます.
さて,この問題を解いてくれた論文が,
です.そもそもは,
を読んでいたのですが,パワースペクトルを計算するときにOddeの論文を引用していました.
このOddeの論文での計算の仕方は独特で,最初は全然わかりませんでしたが,読んでいるうちになかなか面白い手法で解いていることに驚きました.
なかなか頭の良い人がいるものです....
今回は,この波形の自己相関関数がどの様になるか?,を計算していきます.
ポアソン分布
まずは,反応式を見てみましょう. ここでは,Oddeの論文に従って,記号を記します.
\(\hspace{ 30pt } \nu \hspace{ 42pt } \nu \hspace{ 44pt } \nu \\[-5 pt] \Large A_0 \longrightarrow A_1 \longrightarrow \cdots \longrightarrow A_k \)
ここでは,すべての反応速度は等しくてvとしてkステップ起こる逐次反応を考えます.
さて,各反応はランダムに起こりますから,ある一定の時間で起こる確率はポアソン分布に従います.
これがk回起こるのですから,
\(\Large P_k = \frac{(\nu \tau)^k}{k!} e^{- \nu \tau} \)
となります.
ポアソン分布の場合には各イベントがランダムに起こるので,同じ時間に起こっても問題ないですが,逐次反応の場合には連続的(途切れ途切れでも良い)に起こらないとまずいと思います.
しかし,vτがとても小さい値と考えていそうなので,重なって起こる可能性を無視しているのだろうと想像します.
次ページに,進みます.