パワースペクトルの実際の作業内容-07

　単に間引くだけでいいのか？

もう一度おさらいすると，ここ，に示したように，下図にあるように，

　実際の波形の時間 (s)　　：　S_time
　サンプル周波数 (1/s)　　：　S_freq
　サンプル時間分解能 (s)　：　dt
　実際の波形の数　　　　　：　n

とすると，

\(\Large \displaystyle S_{time} = n \times dt = \frac{n}{S_{freq}} \)

の関係になります．これにフーリエ変換すると，

　フーリエ変換の横軸の最小単位 (Hz)　　　：　df
　フーリエ変換の横軸の数　　　　　　　　：　f_number
　フーリエ変換の横軸のレンジ（最大値）　： 　f_range

とすると，

\(\Large \displaystyle df = \frac{S_{freq}}{n} = \frac{1}{S_{time}}\)

\(\Large \displaystyle f_{number} = \frac{n}{2} \)

\(\Large \displaystyle f_{range} = \frac{S_{freq}}{2} \)

となります．

仮に，ひとつずつデータを間引くとすると，実際の波形の時間は変わらないので，

\(\Large \displaystyle S_{time\_D} = S_{time} = n_D \times dt_D = n \times dt = \frac{n_D}{S_{freq\_D}} = \frac{n}{S_{freq}}\)

となります．間引いた結果のパラメータにはDの添え字をつけています．

\(\Large \displaystyle S_{time\_D} = S_{time} \)

なので，一つずつ間引いているので波形のデータ数は半分になるので，

\(\Large \displaystyle n_D = \frac{n}{2} \)

\(\Large \displaystyle n \times dt = n_D \times dt_D = \frac{n}{2} \times dt_D \)

\(\Large \displaystyle dt_D = 2 \ dt \)

となり，サンプル時間分解能が2倍となるのです．また，

\(\Large \displaystyle \frac{n}{S_{freq}} = \frac{n_D}{S_{freq\_D}} = \frac{n}{2} \frac{1}{S_{freq\_D}}\)

\(\Large \displaystyle S_{freq\_D} = \frac{1}{2} S_{freq} \)

とサンプル周波数は半分になります（サンプル時間分解能の逆数だからそうですね）．

df，は，

\(\Large \displaystyle df = \frac{S_{freq}}{n} = \frac{1}{S_{time}}\)

ですが，

\(\Large \displaystyle df_D = \frac{S_{freq\_D}}{n_D} = \frac{ \frac{1}{2} S_{freq}}{ \frac{1}{2} n} = \frac{S_{freq}}{n} = df \)

と変わりません，これで，データを間引くことにより，dfを変えることなくFFTの計算時間を少なくすることができるのです．

・間引くとどうなるか？

では，実際に間引いてみましょう．

元データ
　一様ホワイトノイズ
　実際の波形の時間 (s)　：　S_time = 0.064 s
　サンプル周波数 (1/s)　：　S_freq = 2,000 Hz
　サンプル時間分解能 (s)　：　dt = 0.0005 ms
　実際の波形の数　：　n = 128

で半分にデータ数を間引いていきます（一つずつ間引く）

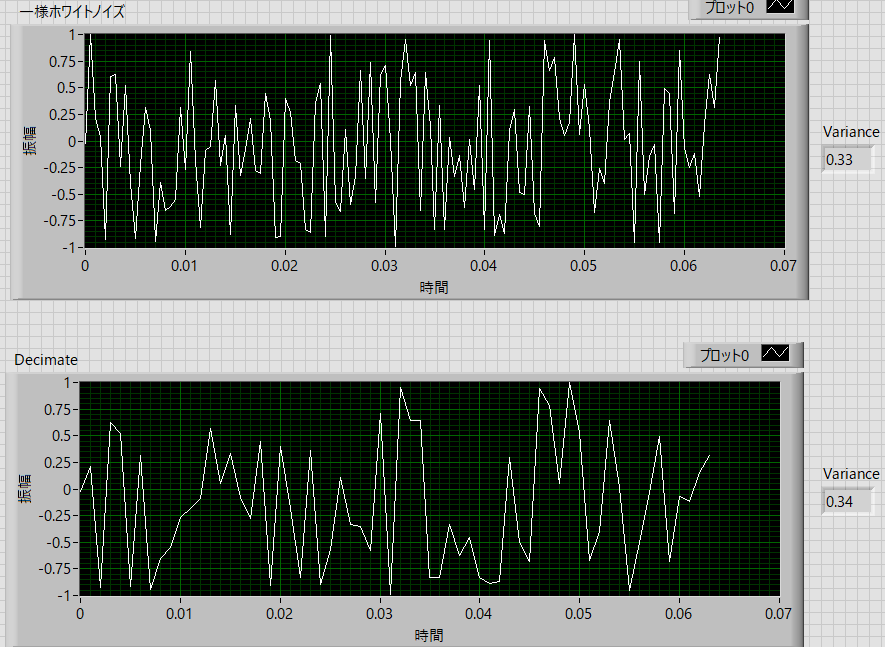
上が，元波形，下が間引いた波形です．

\(\Large \displaystyle S_{time\_D} = S_{time} \)

と変わらないことがわかります．

重要な点は，

　分散値は間引いても変わらない

という点です．

図の右の数字の計算結果のように，
　元波形　　　　：　0.33
　間引いた波形　：　0.34
と同じであることがわかります．

これが結構曲者なのです．