ガンマ分布と逐次反応-02

・3ステップ

計算は，ここ，と同じです．

\( \Large A \xrightarrow{\lambda} B \xrightarrow{\lambda} C \xrightarrow{\lambda} D\)

という状態を考えます．

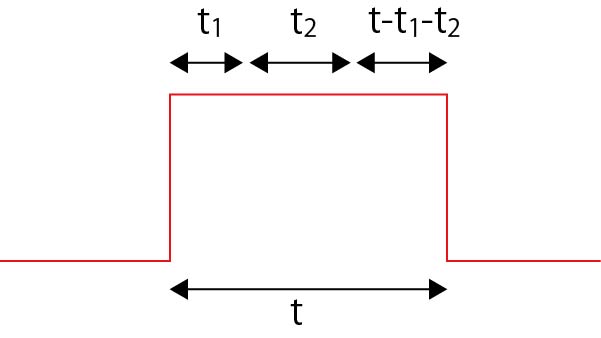
それぞれのステップの時間が，t₁, t₂である時間は，

\( \Large A \xrightarrow{\lambda} B : \lambda e^{- \lambda t_1} \)

\( \Large B \xrightarrow{\lambda} C : \lambda e^{- \lambda t_2} \)

\( \Large C \xrightarrow{\lambda} D : \lambda e^{- \lambda t_3} \)

つまり，t=t₁+t₂+t₃であるためには，

\( \Large t_3 = t - t_1 -t_2 \)

の関係があるので，それぞれの確率の積を，t₂を，0～t₁に渡って，t₁を，0～t-t₁に渡って，積分すればいいのです．

\( \Large  \begin{eqnarray} && \displaystyle \int_{0}^{ t} \displaystyle \int_{0}^{\color{red}{t- t_1}} \lambda e^{- \lambda t_1} \cdot \lambda e^{- \lambda t_2} \cdot \lambda e^{- \lambda (t-t_1-t_2)} dt_2 dt_1 \\
&=& \lambda^3 \displaystyle \int_{0}^{ t} \displaystyle \int_{0}^{\color{red}{t- t_1}} e^{- \lambda t_1} \cdot e^{- \lambda t_2} \cdot e^{- \lambda t} \cdot e^{ \lambda t_1} \cdot e^{ \lambda t_2} dt_2 dt_1\\
&=& \lambda^3 e^{- \lambda t} \cdot \displaystyle \int_{0}^{ t} \displaystyle \int_{0}^{\color{red}{t- t_1}} dt_2 dt_1\\
&=& \lambda^3 e^{- \lambda t} \cdot \displaystyle \int_{0}^{ t} \color{red}{\left( t-t_1 \right)}dt_1\\
&=& \lambda^3 e^{- \lambda t} \cdot \left[\color{red}{ t \cdot t_1 - \frac{1}{2} t_1^2} \right]^t_0 \\
&=& \lambda^3 e^{- \lambda t} \cdot \left(\color{red}{ t^2 - \frac{1}{2} t^2} \right) \\
&=& \lambda^3 e^{- \lambda t} \cdot \color{red}{ \frac{1}{2} t^2} \\
&=& \frac{\lambda^3 \cdot t^2 \cdot e^{- \lambda t} }{2} \\
\end{eqnarray} \)

となります．

次は4ステップ．