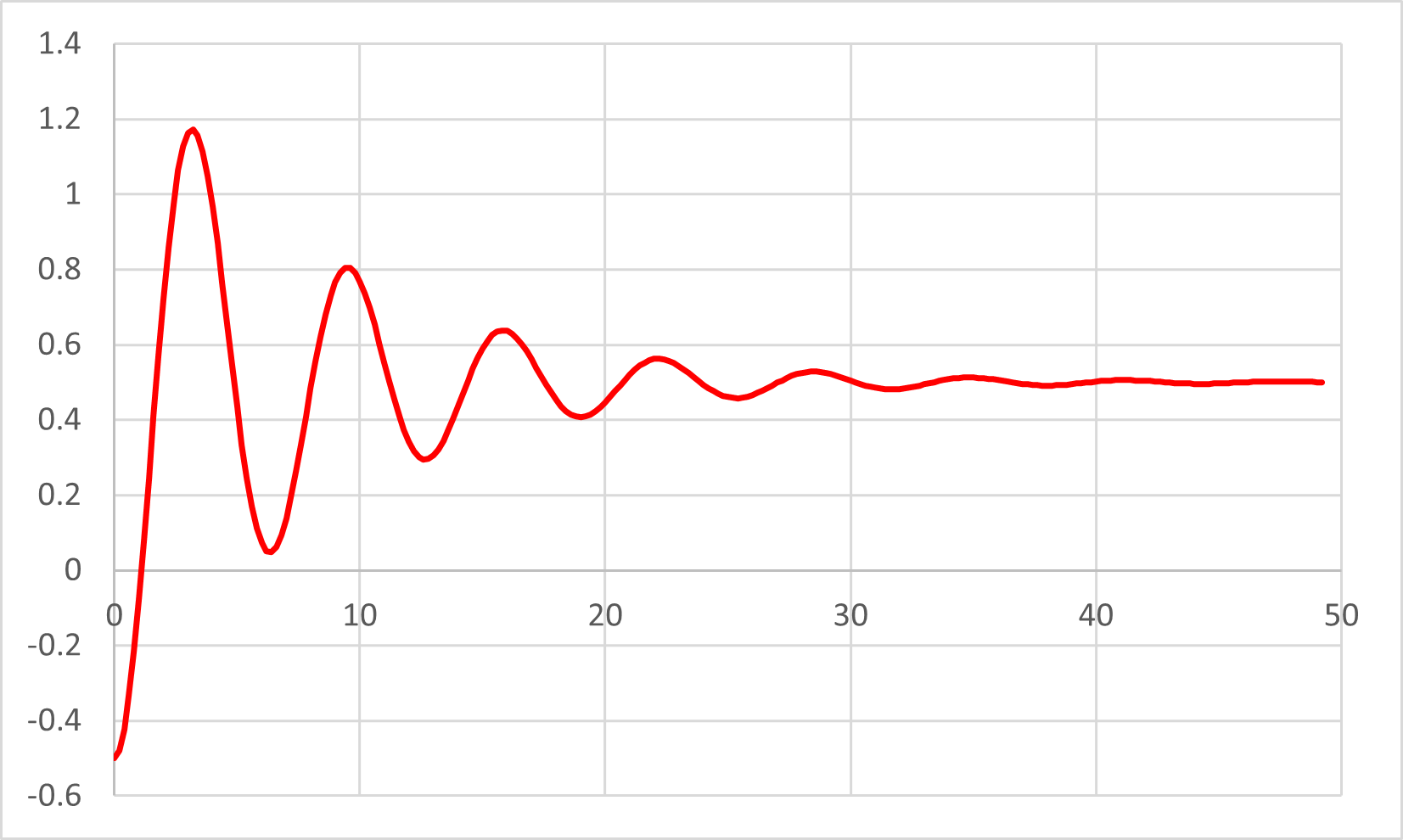
減衰振動_ステップ応答-03

運動方程式からのステップ応答

次に，　任意波形発生器などで矩形波を発生させた時の応答をみていきましょう．
任意波形の場合には標準では±の矩形波となりますので，　初期値が異なります．

初期値

\( \Large t=0, \color {red}{x=-\frac{f}{c}}, \ x'=0 \)

と設定して定数項を計算していきましょう．

\( \Large x = \frac{f}{c} + c_1 \ e^{- (\alpha + j \omega) t} + c_2 \ e^{- (\alpha - j \omega) t}\)

まずは，\( \Large t=0, \color {red}{x=-\frac{f}{c}} \)から．これは簡単で，

\( \Large \color {red}{-\frac{f}{c}} = \frac{f}{c} + c_1 +c_2 \)

\( \Large c_1 +c_2 = -\frac{\color {red}{2} \ f}{c} \)

次に，微分，t=0, x'=0 を計算します．

\( \Large x'(0) = c_1 \ (\alpha + j \omega) + c_2 (\alpha - j \omega) = 0 \)

この二つの連立方程式を解けば，

\( \Large c_1 = \frac{\color {red}{2} \ f}{c} \frac{1}{2j \omega } (\alpha -j \omega) \)

\( \Large c_2= -\frac{\color {red}{2} \ f}{c} \frac{1}{2j \omega } (\alpha + j\omega) \)

となります，したがって，

\( \Large \begin{eqnarray} \Large x
&=& \frac{f}{c} + \frac{\color {red}{2} \ f}{c} \frac{1}{2j \omega} (\alpha - j \omega) e^{- (\alpha + j \omega) t} - \frac{\color {red}{2} \ f}{c} \frac{1}{2j \omega} (\alpha + j \omega) \ e^{- (\alpha - j \omega) t}\\
&=& \frac{f}{c} + \frac{\color {red}{2} \ f}{c} \frac{1}{2j \omega} \left[ (\alpha - j \omega) e^{- (\alpha + j \omega) t} - (\alpha + j \omega) \ e^{- (\alpha - j \omega) t} \right]\\
&=& \frac{f}{c} + \frac{\color {red}{2} \ f}{c} \frac{1}{2j \omega} e^{- \alpha t} \left[ (\alpha - j \omega) e^{- j \omega t} - (\alpha + j \omega) \ e^{ j \omega t} \right]\\
\end{eqnarray} \)

となります．つぎにオイラーの公式から，

\( \Large sin \ x = \frac{ e^{jx} - e^{-jx}}{2j} \)

\( \Large cos \ x = \frac{ e^{jx} + e^{-jx}}{2} \)

を使って，

\( \Large \begin{eqnarray} \Large x
&=& \frac{f}{c} + \frac{\color {red}{2} \ f}{c} \frac{1}{2j \omega} e^{- \alpha t} \left[ \alpha \left( e^{ -j \omega t} - e^{ j \omega t} \right )
- j \omega \left( e^{ -j \omega t} + e^{j \omega t} \right ) \right] \\
&=& \frac{f}{c} + \frac{\color {red}{2} \ f}{c} \frac{1}{2j \omega} e^{- \alpha t} \left[ -2 j \alpha \ sin \omega \ t - 2 j \omega cos \omega \ t \right] \\
&=& \frac{f}{c} - \frac{\color {red}{2} \ f}{c} \frac{1}{\omega} e^{- \alpha t} \left[ \alpha \ sin \omega \ t + \omega cos \omega \ t \right] \\
\end{eqnarray} \)

となります．

ここで，

\( \Large tan \phi \equiv \frac { \omega}{ \alpha} \)

とすれば，

\( \Large sin \phi = \frac{\omega}{ \sqrt{ \alpha^2 + \omega^2}} \)

\( \Large cos \phi = \frac{\alpha}{ \sqrt{ \alpha^2 + \omega^2}} \)

となるので，

\( \Large x = \frac{f}{c} - \frac{\color {red}{2} \ f}{c} \frac{1}{\omega} e^{- \alpha t} \sqrt{ \alpha^2 + \omega^2}
\left[ \ sin \ \omega t \ cos \ \phi + cos \ \omega t \ sin \ \phi \right] \)

となります．

つぎに三角関数の公式から，

\( \Large sin (A + B ) =sin A cos B + cos A sin B \)

を使って，

\( \Large \begin{eqnarray} x
&=& \frac{f}{c} - \frac{\color {red}{2} \ f}{c} \frac{1}{\omega} e^{- \alpha t} \sqrt{ \alpha^2 + \omega^2}\ sin ( \omega t + \phi ) \\
&=& \frac{f}{c} \left[ 1 - \color {red}{2} \sqrt{ 1 + \frac{\alpha^2}{\omega^2}} \ e^{- \alpha t} \ sin ( \omega t + \phi ) \right] \\
\end{eqnarray} \)

となります．

前ページの初期値と比べるとこのような違いとなります．

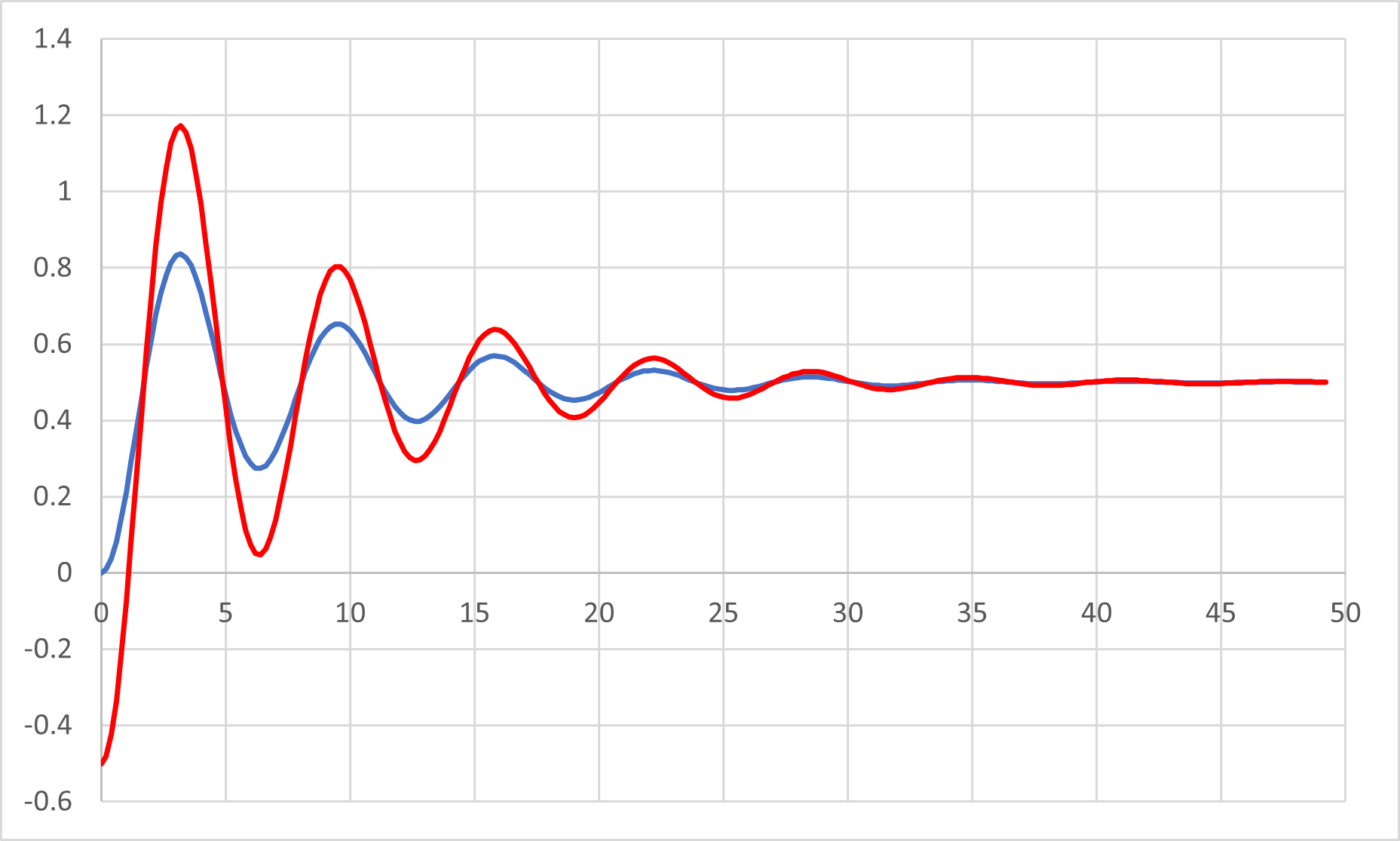
次に，運動方程式，RLC回路において，具体的なパラメータを入れて考えていきましょう．