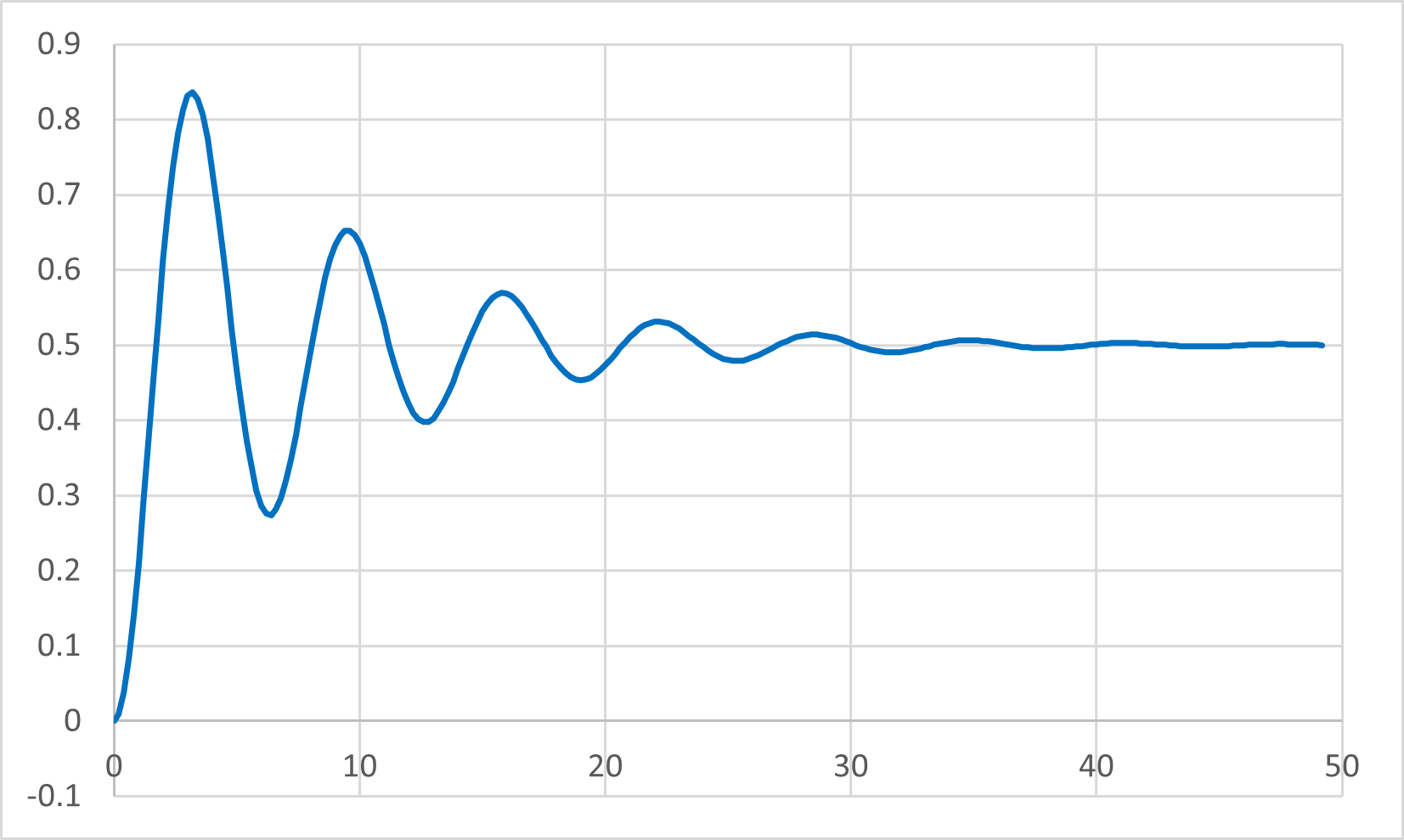
減衰振動_ステップ応答-02

運動方程式からのステップ応答

初期値 ( t=0, x=x'=0 )

\( \Large t=0, x=x'=0 \)

と設定して定数項を計算していきましょう．

\( \Large x = \frac{f}{c} + c_1 \ e^{- (\alpha + j \omega) t} + c_2 \ e^{- (\alpha - j \omega) t}\)

まずは，t=0, x=0から．これは簡単で，

\( \Large 0 = \frac{f}{c} + c_1 +c_2 \)

\( \Large c_1 +c_2 = -\frac{f}{c} \)

次に，微分，t=0, x'=0 を計算します．

\( \Large x'(0) = c_1 \ (\alpha + j \omega) + c_2 (\alpha - j \omega) = 0 \)

この二つの連立方程式を解けば，

\( \Large c_1 = \frac{f}{c} \frac{1}{2j \omega } (\alpha -j \omega) \)

\( \Large c_2= -\frac{f}{c} \frac{1}{2j \omega } (\alpha + j\omega) \)

となります，したがって，

\( \Large \begin{eqnarray} \Large x
&=& \frac{f}{c} + \frac{f}{c} \frac{1}{2j \omega} (\alpha - j \omega) e^{- (\alpha + j \omega) t} - \frac{f}{c} \frac{1}{2j \omega} (\alpha + j \omega) \ e^{- (\alpha - j \omega) t}\\
&=& \frac{f}{c} + \frac{f}{c} \frac{1}{2j \omega} \left[ (\alpha - j \omega) e^{- (\alpha + j \omega) t} - (\alpha + j \omega) \ e^{- (\alpha - j \omega) t} \right]\\
&=& \frac{f}{c} + \frac{f}{c} \frac{1}{2j \omega} e^{- \alpha t} \left[ (\alpha - j \omega) e^{- j \omega t} - (\alpha + j \omega) \ e^{ j \omega t} \right]\\
\end{eqnarray} \)

となります．つぎにオイラーの公式から，

\( \Large sin \ x = \frac{ e^{jx} - e^{-jx}}{2j} \)

\( \Large cos \ x = \frac{ e^{jx} + e^{-jx}}{2} \)

を使って，

\( \Large \begin{eqnarray} \Large x
&=& \frac{f}{c} + \frac{f}{c} \frac{1}{2j \omega} e^{- \alpha t} \left[ \alpha \left( e^{ -j \omega t} - e^{ j \omega t} \right )
- j \omega \left( e^{ -j \omega t} + e^{j \omega t} \right ) \right] \\
&=& \frac{f}{c} + \frac{f}{c} \frac{1}{2j \omega} e^{- \alpha t} \left[ -2 j \alpha \ sin \omega \ t - 2 j \omega cos \omega \ t \right] \\
&=& \frac{f}{c} - \frac{f}{c} \frac{1}{\omega} e^{- \alpha t} \left[ \alpha \ sin \omega \ t + \omega cos \omega \ t \right] \\
\end{eqnarray} \)

となります．

ここで，

\( \Large tan \phi \equiv \frac { \omega}{ \alpha} \)

とすれば，

\( \Large sin \phi = \frac{\omega}{ \sqrt{ \alpha^2 + \omega^2}} \)

\( \Large cos \phi = \frac{\alpha}{ \sqrt{ \alpha^2 + \omega^2}} \)

となるので，

\( \Large x = \frac{f}{c} - \frac{f}{c} \frac{1}{\omega} e^{- \alpha t} \sqrt{ \alpha^2 + \omega^2}
\left[ \ sin \ \omega t \ cos \ \phi + cos \ \omega t \ sin \ \phi \right] \)

となります．

つぎに三角関数の公式から，

\( \Large sin (A + B ) =sin A cos B + cos A sin B \)

を使って，

\( \Large \begin{eqnarray} x
&=& \frac{f}{c} - \frac{f}{c} \frac{1}{\omega} e^{- \alpha t} \sqrt{ \alpha^2 + \omega^2}\ sin ( \omega t + \phi ) \\
&=& \frac{f}{c} \left[ 1 - \sqrt{ 1 + \frac{\alpha^2}{\omega^2}} \ e^{- \alpha t} \ sin ( \omega t + \phi ) \right] \\
\end{eqnarray} \)

となります．

次に，任意波形発生器，のように，±X，のようなステップの場合の応答を考えていきましょう