減衰振動-04

運動方程式からの減衰振動

γ ＝ ω₀ の場合　（臨界減衰）

この場合には，

\( \Large x = e^{- \gamma t} \left[ A \ e^{ \sqrt{\gamma^2 - \omega_0^2} t} +B \ e^{ - \sqrt{\gamma^2 - \omega_0^2} t} \right] 　\)

において，平方根の中が0となりますので，簡単に，

\( \Large x = e^{- \gamma t} 　\)

となります．

これも一つの独立解ですが，もう一つの解を求める必要があります．

その詳細については，ここ，をご覧ください．

その解き方は，（ここ，を参考にしました）

\( \Large \frac{d^2 x}{dt^2} +2 \gamma \frac{dx}{dt} +\omega_0^2 x =0 \)

において，γ²＝ω₀²なので，

\( \Large \frac{d^2 x}{dt^2} +2 \gamma \frac{dx}{dt} +\gamma^2 x =0 \)

を解くことになります．　

このとき，一つの解は，先に出た，

\( \Large x_1 = e^{- \gamma t} 　\)

となります．このxとは独立な解を見つける必要があります．それには，定数変化法が有効で，

\( \Large x_2 = C(t) \ x_1(t) = C(t) e^{- \gamma t} 　\)

これを先の式に代入します．

\( \Large \frac{d^2 x}{dt^2} +2 \gamma \frac{dx}{dt} +\gamma^2 x =0 \)

\( \begin{eqnarray} && \left[ C''(t) x_1(t)+2C'(t) x'_1(t)+C(t) x_1''(t) \right] + 2 \gamma \left[ C'(t) x_1(t)+C(t) x'_1(t) \right] +\gamma^2 C(t) x_1(t) \\
&=& C(t) \left[ x_1''(t) + 2 \gamma x'_1(t) + \gamma^2 x_1(t) \right] + \left[ C''(t) x_1(t)+2C'(t) x'_1(t) + 2 \gamma C'(t) x_1(t) \right] \\
\end{eqnarray}　\)

となります．

第一項は先の微分方程式と一致するので，0となります．従って，

\( \Large C''(t) x_1(t)+2C'(t) x'_1(t) + 2 \gamma C'(t) x_1(t) =0 　\)

\( \Large x_1 = e^{- \gamma t} 　\)　なので，

\( \Large \begin{eqnarray}　&& C''(t) x_1(t)+2C'(t) x'_1(t) + 2 \gamma C'(t) x_1(t) \\
&=& C''(t) e^{- \gamma t}-2 \gamma C'(t) e^{- \gamma t} + 2 \gamma C'(t) e^{- \gamma t} \\
&=& C''(t) e^{- \gamma t} \\
&=& 0 \\
\end{eqnarray}　\)

つまり，

\( \Large C''(t) e^{- \gamma t} = 0　\)　

\( \Large C''(t) = 0　\)　

となります．

\( \Large C'(t) = D_2　\)

\( \Large C(t) = D_2 t + D_1　\)

となるので，

\( \Large x_2 = ( D_2 t + D_1 ) e^{- \gamma t }　\)

まとめると，

\( \Large \begin{eqnarray} x &=& x_1 +x_2 \\
&=& D_0 e^{- \gamma t } + ( D_2 t + D_1 ) e^{- \gamma t }　\\
&=& ( D_2 t + D ) e^{- \gamma t }　\\
\end{eqnarray}　\)

初期条件として

\( \Large t=0 \quad -> \quad x=1 \)

\( \Large t=0 \quad -> \quad x'=0 \)

とします．

・　\( \Large t=0 \quad -> \quad x=1 \)

\( \Large 1 = D　\)

・　\( \Large t=0 \quad -> \quad x'=0 \)

\( \Large x' = - \gamma ( D_2 t + D ) e^{- \gamma t }+ D_2 e^{- \gamma t }　　\)

\( \Large 0 = - \gamma \ D+ D_2 \)

\( \Large D_2 = \gamma \)

つまり，

\( \Large x = ( \gamma t + 1) e^{- \gamma t }　　\)

となります．

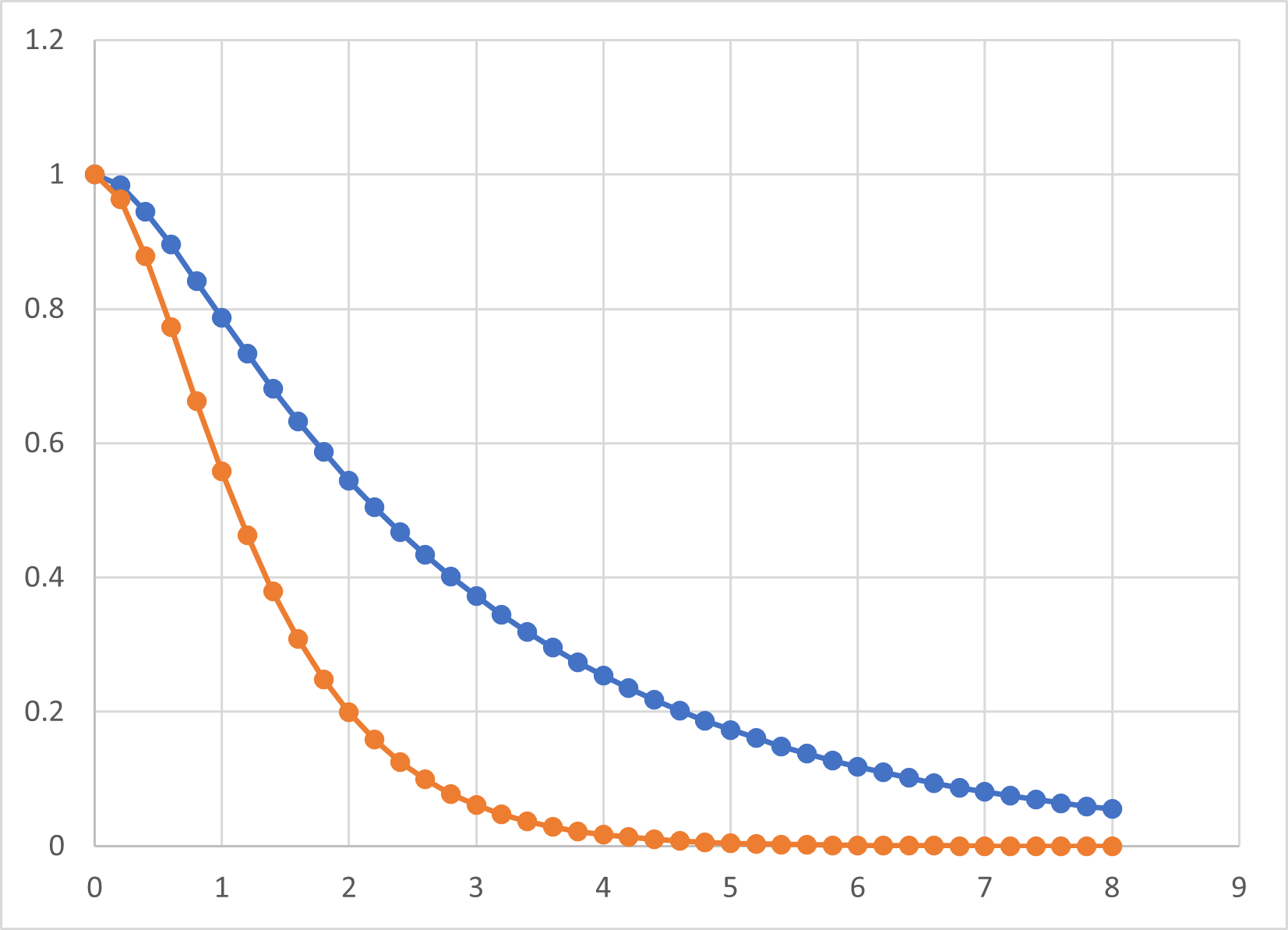
γ > ω₀とγ = ω₀とを比較してみると，

青：γ > ω₀
オレンジ：γ= ω₀

であり，臨界減衰が早く減衰することが分かります．

次に，ステップ変位に対する応答を見ていきましょう．