減衰振動-03

運動方程式からの減衰振動

γ ＜ ω₀ の場合　（減衰振動）

この場合には，
\( \Large \gamma = \frac{b}{2m} \)

\( \Large \omega_0 = \sqrt{\frac{K}{m}} \)

なので，
　平方根の中がマイナス　＝　虚数項が発生する
ことになります，これは，
　粘性抵抗係数　＜　弾性率
の場合に相当します，つまり，粘性がほとんど無視できる状況とイメージしてもらえればいいかと思います．

そこで，

\( \Large \sqrt{\gamma^2 - \omega_0^2} = i \ \sqrt{\omega_0^2 - \gamma^2} = i \ \omega 　\)

とおくと，

\( \Large x = e^{- \gamma t} \left[ A \ e^{ i \ \omega t} +B \ e^{ - i \ \omega t } \right] 　\)

と簡単になります．

オイラーの公式，

\( \Large e^{ \pm i \theta} = cos \theta \pm i \ sin \theta　\)

と使って，

\( \Large \begin{eqnarray} x &=& e^{- \gamma t} \left[ A \ \left( cos \omega t + i \ sin \omega t \right) +B \ \left( cos \omega t - i \ sin \omega t \right) \right] \\
&=& e^{- \gamma t} \left[ (A+B) \ cos \omega t + i \ (A-B) \ sin \omega t \right] \\
\end{eqnarray}　\)

物理量ｘが実数であることから，

\( \Large A = \frac{C_1-i C_2}{2}　\)

\( \Large B = \frac{C_1+i C_2}{2}　\)

とおくと，

\( \Large \begin{eqnarray} x &=& e^{- \gamma t} \left[ (A+B) \ cos \omega t + i \ (A-B) \ sin \omega t \right] \\
&=& e^{- \gamma t} \left[ C_1 \ cos \omega t + C_2 \ sin \omega t \right] \\
\end{eqnarray}　\)

ここで，

\( \Large C = \sqrt{C_1^2+ C_2^2}　\)

\( \Large cos \alpha = \frac{C_1}{C}　\)

\( \Large sin \alpha = -\frac{C_2}{C}　\)

とすると，先ほどの式は，

\( \Large \begin{eqnarray} x &=& e^{- \gamma t} \left[ C_1 \ cos \omega t + C_2 \ sin \omega t \right] \\
&=& e^{- \gamma t} \left[ C \ cos \alpha \ cos \omega t + C \ sin \alpha \ sin \omega t \right] \\
&=& C \ e^{- \gamma t} \left[ cos \alpha \ cos \omega t - sin \alpha \ sin \omega t \right] \\
\end{eqnarray}　\)

となります．

三角関数の加法定理，

\( \Large cos \alpha \ cos \beta - sin \alpha \ sin \beta = cos ( \alpha +\beta) \)

より，

\( \Large x = C \ e^{- \gamma t} cos ( \omega t + \alpha )\)

となります．

つまり，
　減衰する指数項
　振動する三角関数項
の積となるのです．

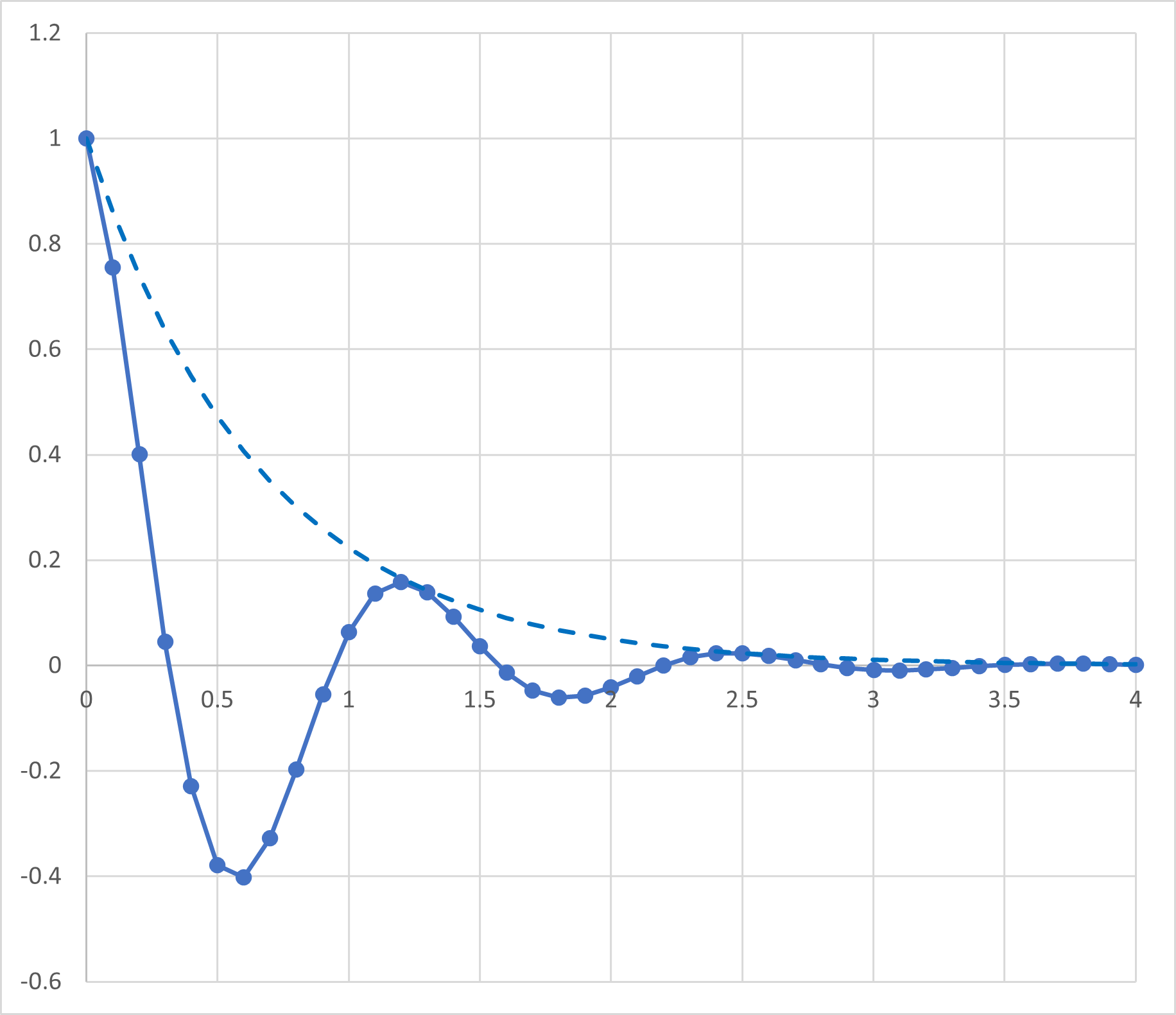
図示すると，

のようになります．
　実線：　\( \Large x = C \ e^{- \gamma t} cos ( \omega t + \alpha ) \)
　点線：　\( \Large x = C \ e^{- \gamma t} \)

となります，振動しながら減衰していく様子が分かります．

ちょうど振り子の振動が徐々に小さくなってくる様子です．

次のページに，γ＝ω₀の場合についての計算を行います．