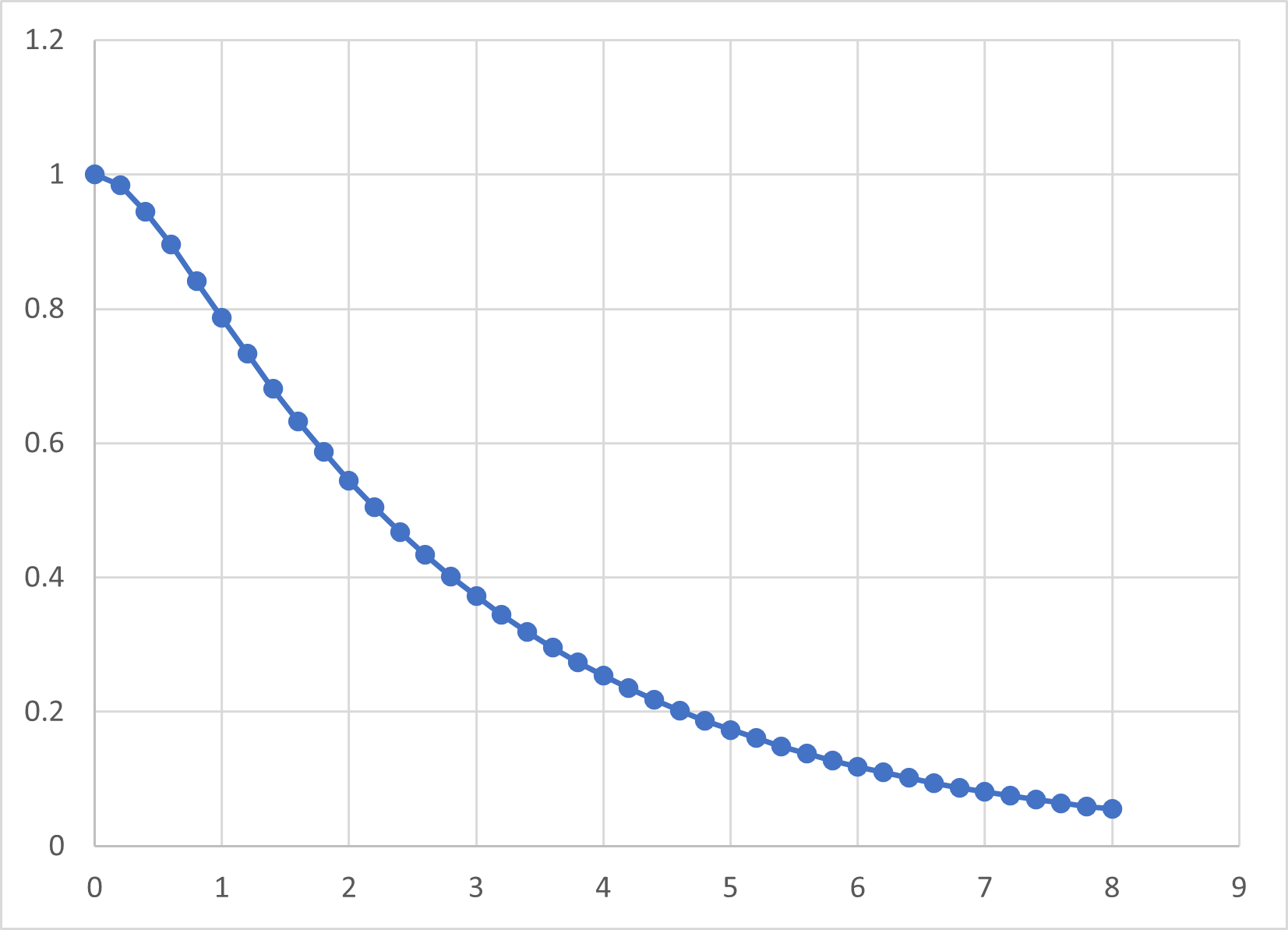
減衰振動-02

運動方程式からの減衰振動

γ > ω₀ の場合　（過減衰）

この場合には，
\( \Large \gamma = \frac{b}{2m} \)

\( \Large \omega_0 = \sqrt{\frac{K}{m}} \)

なので，
　粘性抵抗係数　＞　弾性率
の場合に相当します，つまり，ドロドロの溶液中とイメージしてもらえればいいかと思います．

すると，

\( \Large \sqrt{\gamma^2 - \omega_0^2} \)

が実数となります．従って，振動せずに単調減少となります．

\( \Large x = e^{- \gamma t} \left[ A \ e^{ \sqrt{\gamma^2 - \omega_0^2} t} +B \ e^{ - \sqrt{\gamma^2 - \omega_0^2} t} \right] 　\)

定数，A，Bを見積もってみましょう．（ここ，を参考）

初期条件として，

\( \Large t=0 \quad -> \quad x=1 \)

\( \Large t=0 \quad -> \quad x'=0 \)

とします．

・　\( \Large t=0 \quad -> \quad x=1 \)

\( \Large 1 = A + B　\)

・　\( \Large t=0 \quad -> \quad x'=0 \)

\( \Large x' = - \gamma e^{- \gamma t} \left[ A \ e^{ \sqrt{\gamma^2 - \omega_0^2} t} +B \ e^{ - \sqrt{\gamma^2 - \omega_0^2} t} \right] + e^{- \gamma t} \left[ A \ \sqrt{\gamma^2 - \omega_0^2} \ e^{ \sqrt{\gamma^2 - \omega_0^2} t} -B \ \sqrt{\gamma^2 - \omega_0^2} \ e^{ - \sqrt{\gamma^2 - \omega_0^2} t} \right] 　\)

\( \Large 0 = - \gamma \left[ A +B \right] + \left[ A \ \sqrt{\gamma^2 - \omega_0^2} -B \ \sqrt{\gamma^2 - \omega_0^2} \right] 　\)

\( \Large \gamma = \sqrt{\gamma^2 - \omega_0^2} \left[ A -B \right] 　\)

\( \Large A-B = \frac{ \gamma}{\sqrt{\gamma^2 - \omega_0^2}}　\)

\( \Large A + B=1　\)　から，

\( \Large A = \frac{1}{2} \left[ 1+\frac{ \gamma}{\sqrt{\gamma^2 - \omega_0^2}} \right]　\)

\( \Large B = \frac{1}{2} \left[ 1-\frac{ \gamma}{\sqrt{\gamma^2 - \omega_0^2}} \right]　\)

\( \Large x = \frac{1}{2} e^{- \gamma t} \left[ \lbrace 1+\frac{ \gamma}{\sqrt{\gamma^2 - \omega_0^2}} \rbrace \ e^{ \sqrt{\gamma^2 - \omega_0^2} t} + \lbrace 1-\frac{ \gamma}{\sqrt{\gamma^2 - \omega_0^2}} \rbrace \ e^{ - \sqrt{\gamma^2 - \omega_0^2} t} \right] 　\)

単純な指数関数ではないですが，単調減少となります．

弾性力が無視できるような環境では，ω＝0，と考えていいので，

\( \Large x = e^{- \gamma t} \left[ A \ e^{ \gamma t} +B \ e^{ - \gamma t} \right] 　\)

\( \Large \begin{eqnarray} x &=& e^{- \gamma t} \frac{e^{ \gamma t}}{e^{ \gamma t}} \left[ A \ e^{ \gamma t} +B \ e^{ - \gamma t} \right] 　\\
&=& e^{- 2\gamma t} \left[ A \ e^{ 2 \gamma t} +B \right] \\
&=& A + B e^{- 2\gamma t} \\
\end{eqnarray}　\)

時刻無限大，で減衰して0となりますので，

\( \Large t = \infty \quad -> \quad x=0 　\)

\( \Large 0 = A 　\)

\( \Large x = B e^{- 2\gamma t}\)

時刻，t=0，でx=1，とすると，

\( \Large t = 0 \quad -> \quad x=1 　\)

\( \Large 1 = B \)

\( \Large x = e^{- 2\gamma t}\)

となります．

\( \Large \gamma = \frac{b}{2m} \)

ですので，

\( \Large x = e^{- \frac{b}{m} t}\)

となります．

次のページに，γ＜ω₀の場合についての計算を行います．