RLC回路-02

\( \Large \left( \frac {R}{2L} \right) ^2 > \frac{1}{LC} \)の場合　（過減衰）

この場合には，
\( \Large \left( \frac {R}{2L} \right) ^2 > \frac{1}{LC} \)

\( \Large R ^2 > \frac{4L}{C} \)

となります．すると，

\( \Large \sqrt { \left( \frac {R}{2L} \right) ^2 - \frac{1}{LC}} \)

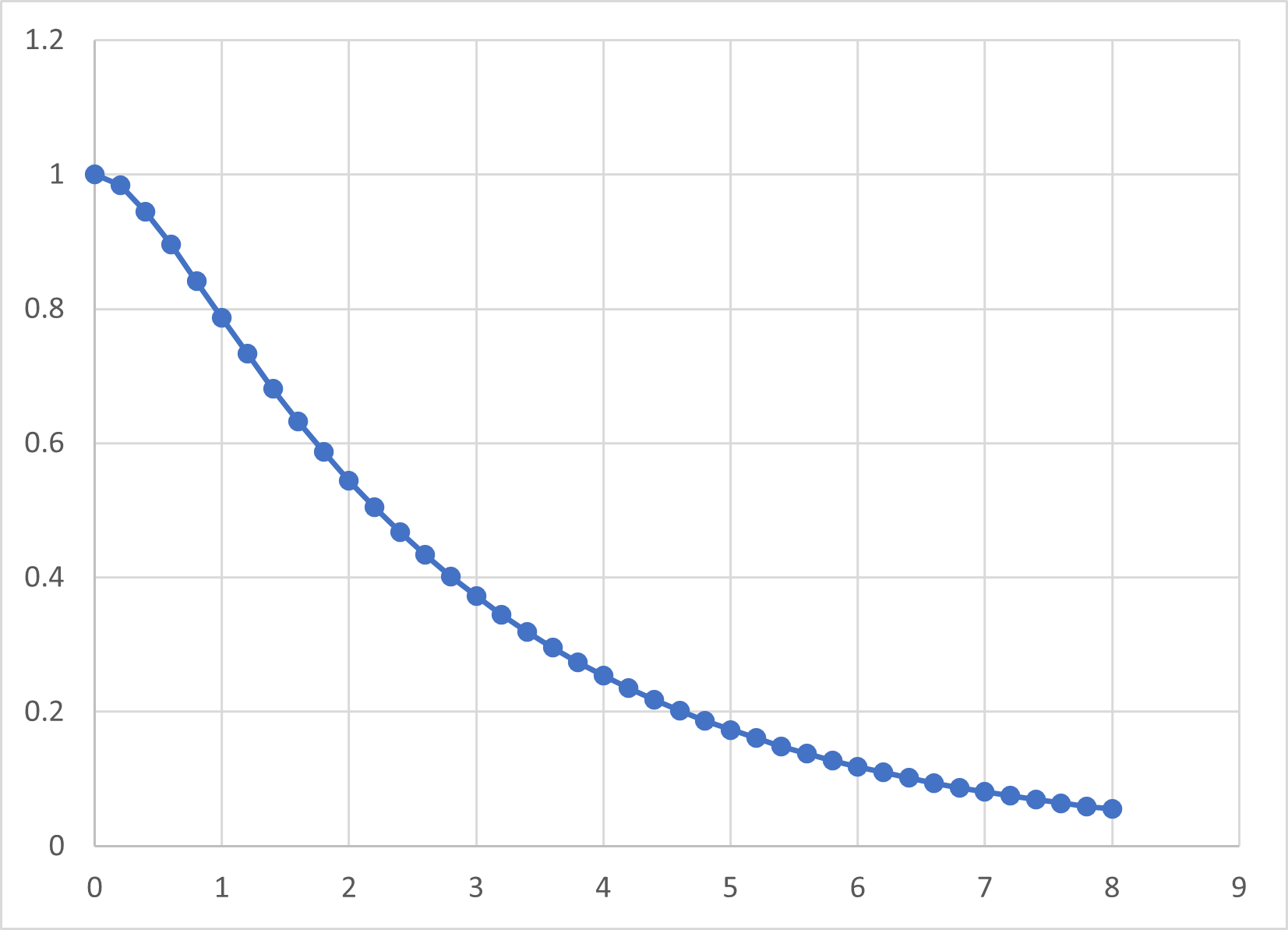
が実数となります．従って，振動せずに単調減少となります．

\( \Large x = e^{- \frac{R}{2L}t} \left[
A \ e^{ \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t }
+B \ e^{ - \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}}t}
\right] 　\)

定数，A，Bを見積もってみましょう．（ここ，を参考）

初期条件として，

\( \Large t=0 \quad -> \quad x=1 \)

\( \Large t=0 \quad -> \quad x'=0 \)

とします．

・　\( \Large t=0 \quad -> \quad x=1 \)

\( \Large 1 = A + B　\)

・　\( \Large t=0 \quad -> \quad x'=0 \)

\( x' = -\frac{R}{2L} e^{- \frac{R}{2L}t} \left[
A \ e^{ \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t }
+B \ e^{ - \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}}t}
\right] 　
+ e^{- \frac{R}{2L}t} \left[
A \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} e^{ \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t }
- B \ \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} e^{ - \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}}t}
\right] 　\)

\( \Large 0 = -\frac{R}{2L} (A +B )　
+ A \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} - B \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}}
　\)

\( \Large \frac{R}{2L} =
(A-B) \sqrt{\left( \frac {2L}{R} \right) ^2 -\frac{1}{LC}}
　\)

すなわち，

\( \Large A-B = \frac{R}{2L \sqrt{\left( \frac {2L}{R} \right) ^2 -\frac{1}{LC}} }
　\)

\( \Large A + B = 1　\)

となるので，

\( \Large A = \frac{1}{2} \left[ 1 + \frac{R}{2L \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} } \right]
　\)

\( \Large B = \frac{1}{2} \left[ 1 - \frac{R}{2L \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} } \right]
　\)

となります，結果的に，

\( x = e^{- \frac{R}{2L}t} \left[
\frac{1}{2} \lbrace 1 + \frac{R}{2L \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} } \rbrace\
e^{ \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t }
+\frac{1}{2} \lbrace 1 - \frac{R}{2L \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} } \rbrace\
e^{ - \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}}t}
\right] 　\)

となります．順番を入れ替えると，

\( \begin{eqnarray} x &=& e^{- \frac{R}{2L}t} \frac{1}{2} \left[ \left(
e^{ \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t}
-e^{ -\sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t} \right)
+ \frac{R}{2L \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}}} \left(
e^{ \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t}
+e^{ -\sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t} \right)
\right] \\
&=& e^{- \frac{R}{2L}t} \ \left[
cosh ( \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t)
+ \frac{R}{2L \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}}} sinh ( \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t)
\right] \\
\end{eqnarray} \)

と書き換えることができます，ここで，双曲線関数

\( \Large cosh x = \frac{e^x + e^{-x}}{2} 　\)

\( \Large sinh x = \frac{e^x - e^{-x}}{2} 　\)

を使いました．

単純な指数関数ではないですが，単調減少となります．

次のページに，\( \Large R ^2 < \frac{4L}{C} \)の場合についての計算を行います．