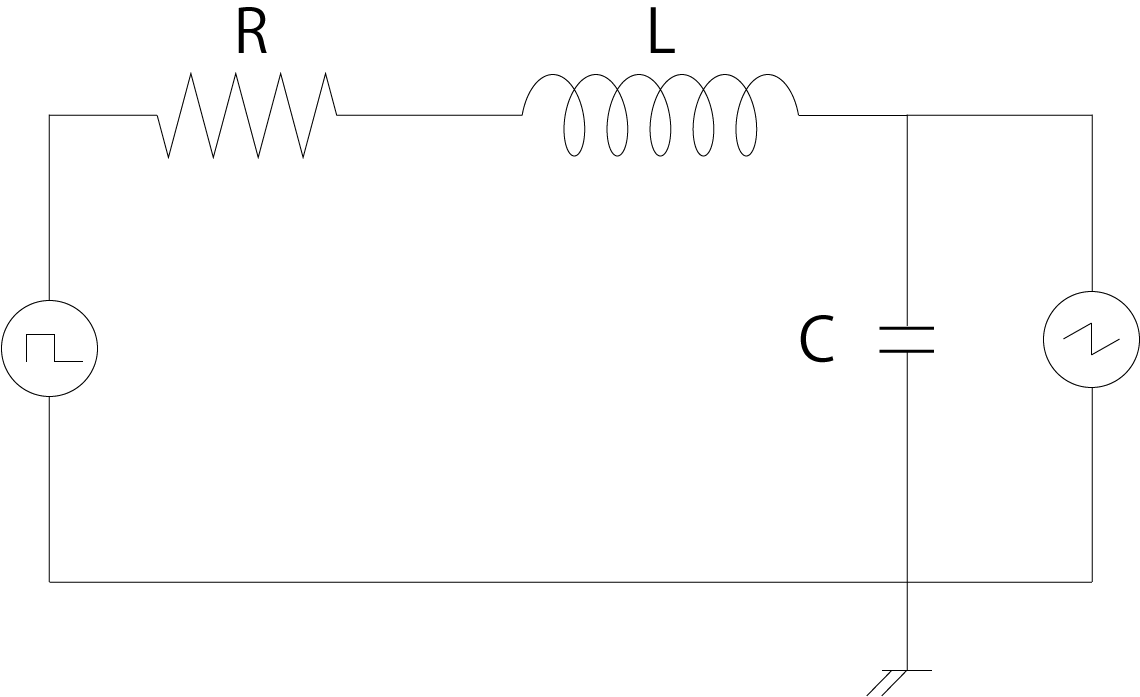
RLC回路-01
電気回路でRLC回路について考えていきましょう.

RLC回路には,
抵抗
コイル
コンデンサ
が含まれています.これらの回路は,以下の式で表すことができます.
\( \Large RI + L \frac{dI}{dt} + \frac{1}{C} \int I dt = V \)
ここで,
I:電流
V:電圧
です.
この式を時間tで微分すると,
\( \Large R \frac{dI}{dt} + L \frac{d^2I}{dt^2} + \frac{I}{C} = 0 \)
並び替えると,
\( \Large L \frac{d^2I}{dt^2} + R \frac{dI}{dt} + \frac{I}{C} = 0 \)
となります.
これは,まさしく,運動方程式ですね.
\( \Large L = m, \quad R =b, \quad \frac{1}{C} = K \)
という対応となります.書き換えて,
\( \Large \frac{d^2I}{dt^2} + \frac{R}{L} \frac{dI}{dt} + \frac{I}{LC} = 0 \)
ここで,この式の解が,\( \Large e^{\lambda t} \) となるとします.
これは,1階,2階,そのままの項が式の中に入っているからです.
微分しても同じもの,と考えると指数関数が妥当だと推定できます.
厳密は説明は,ここ,に詳しく記載されていますので参考にしてみてください.
\( \Large e^{\lambda t} \) を先ほどの式に代入すると,
\( \Large \lambda^2 e^{\lambda t} + \frac{R}{L} \lambda e^{\lambda t} + \frac{1}{LC}e^{\lambda t} =0 \)
となります.両辺を\( \Large e^{\lambda t} \)で割ると,
\( \Large \lambda^2 + \frac{R}{L} \lambda +\frac{1}{LC} =0 \)
と普通の方程式となります.方程式の公式,
\( \Large a x^2 +b x +c=0 \)
\( \Large x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \)
から,
\( \Large \lambda = - \frac{R}{2L} \pm \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} \)
となります.
±の二つの解があり,定数(初期値に依存)を加えてその和が解となりますので,
\( \Large x = A \ e^{ \left( - \frac{R}{2L} + \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} \right) t } \)
\( \Large x = B \ e^{ \left( - \frac{R}{2L} - \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} \right) t} \)
\( \Large \begin{eqnarray} x
&=& A \ e^{ \left( - \frac{R}{2L} + \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} \right) t }
+B \ e^{ \left( - \frac{R}{2L} - \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} \right) t} \\
&=&
e^{- \frac{R}{2L}t} \left[
A \ e^{ \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t }
+B \ e^{ - \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}}t}
\right] \\
\end{eqnarray} \)
この式は,平方根の中が,正,負,0によってその性質は大きく変わります.
次のページに,それぞれの場合についての計算を行います.