Labviewによる非線形近似での各推定値の誤差計算-01

今まで何回か，このサイトに，線形・非線形近似における各推定値の誤差の計算を行ってきました．

いまのところ．．．．

　Python, R, Kyplot，で計算するのが一番簡単

　線形近似においては，エクセルでも十分対応可能

ということでしたが，

　Labviewの非線形近似でも計算可能！

ということがわかりましたので，説明していきたいと思います．

・Labviewのプログラム

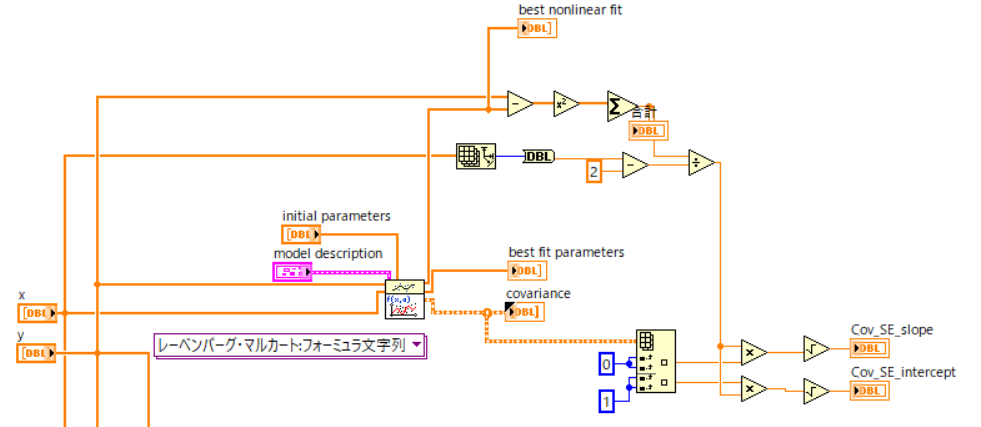
実際のLabviewのブロックダイヤグラムは，以下の通りです．

つまり，

　非線形近似アイコンの，共分散

を利用するのです．フロントパネルでは，

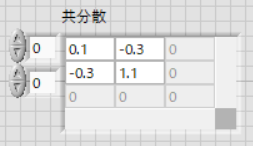
となっており，このうち，(0,0)=0.1, (1,1)=1.1

を使います．ただ，

　なんでこの値を使うと，推定誤差を計算できるのか．．．．よくわからない

という情けなさがありますが，とりあえず使えそうです．

・具体的な計算方法

この共分散の対角にある値を，

\( \Large Cov_{i,i} \)

とします．

そして，ｙの推定値を，

\( \Large \hat{y} \)

とします．

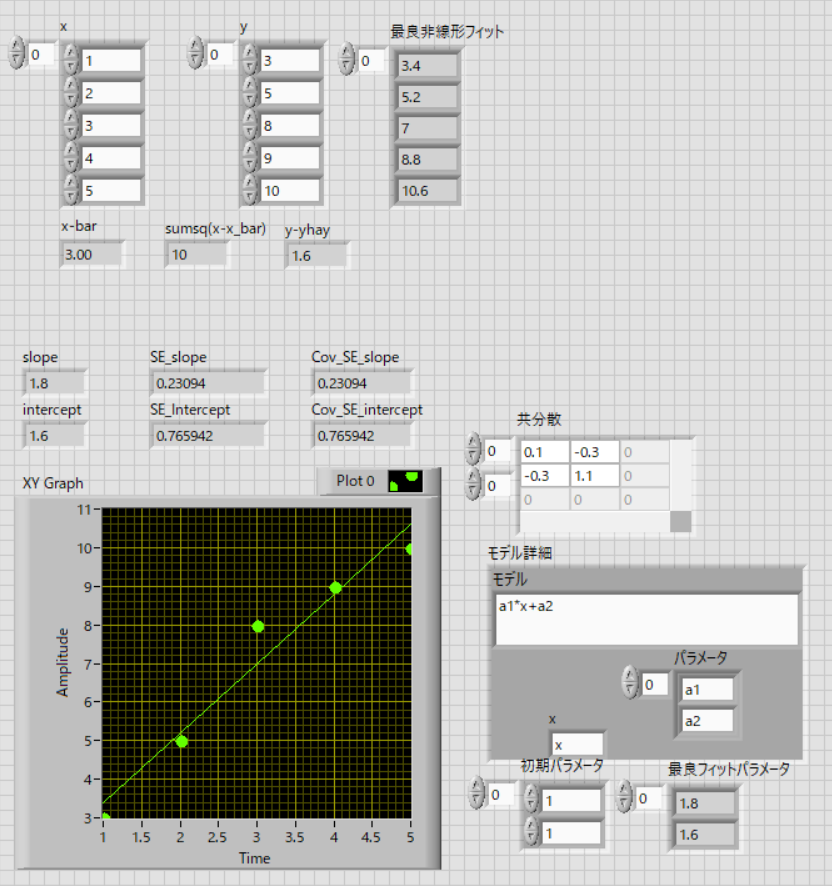
Labviewでの計算は，

\( \Large SE_a = \displaystyle \sqrt{ \frac{ \sum ( y - \hat{y})^2}{n-2} \times Cov_{0,0}} = \sqrt{ \frac{ 1.6}{5-2} \times 0.1} = 0.23094 \)

\( \Large SE_b = \displaystyle \sqrt{ \frac{ \sum ( y - \hat{y})^2}{n-2} \times Cov_{1,1}} = \sqrt{ \frac{ 1.6}{5-2} \times 1.1} = 0.76594 \)

と真面目に計算した結果，と一致します．

真面目な計算の式，は，

\( \Large \displaystyle SE_a =\sqrt{\frac{\sigma_a^2}{n-p}} \)

\( \Large \displaystyle SE_b =\sqrt{\frac{\sigma_b^2}{n-p}} \)

となります．線形近似の場合にはパラメータが2個なので，p=2

\( \Large \displaystyle \sigma_a^2 = \displaystyle \frac{ \sigma_y^2}{S_{xx}} \)

\( \Large \displaystyle \sigma_b^2 =\sigma_y^2 \left\{ \frac{1}{n}+ \frac{\left( \bar{x} \right)^2 }{S_{xx}} \right\} \)

\( \Large \displaystyle \sigma_y^2 = \sum_{i=1}^N ( y_i - \hat{y})^2 \)

となるので，傾き，a，の推定量に関していえば，

\( \Large Cov_{0,0} = \displaystyle \frac{1}{S_{xx}} \)

となるようです．

では，非線形の場合にも，この計算が成り立つかを，次ページ，でトライしてみましょう．