Labviewによる非線形近似での各推定値の誤差計算-01
つぎは,
指数関数 + 一定値
\( \Large a1*exp(-a2*x)+a3 \)
です.
蛍光の退色(背景光あり),などの場合によく使われる計算式です.
エクセルでは,指数近似(対数にして直線近似)がありますが,一定値を含む場合には適用できません.
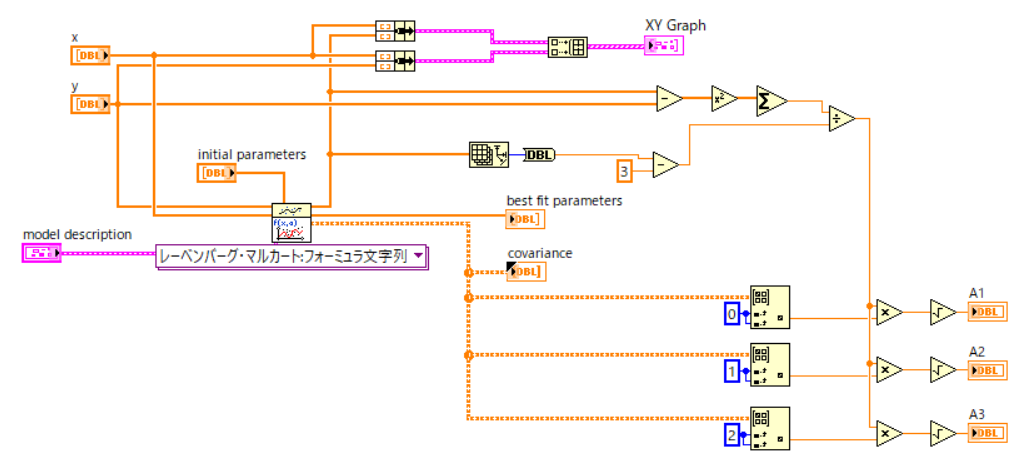
実際のLabviewでのブロックダイヤグラムは,

となり,前ページ同様,共分散とyの推定値とyの差分値を使っています.
フロントパネルは,
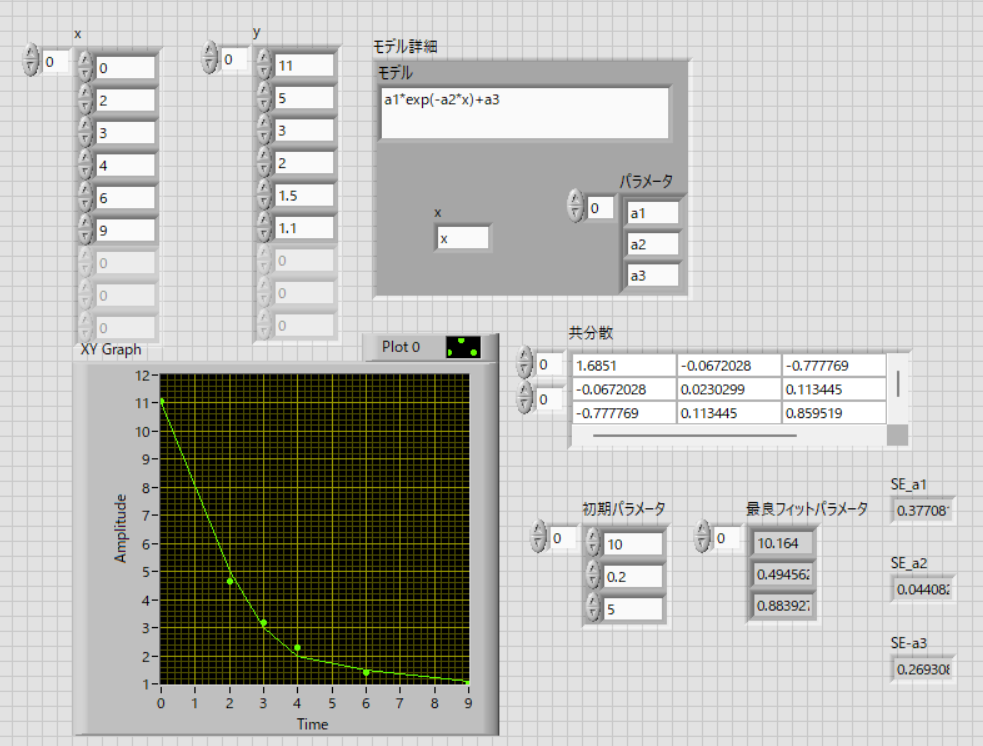
となり,推定値を計算できていて,
\( \Large SE_{a1} = 0.37708 \)
\( \Large SE_{a2} = 0.04408 \)
\( \Large SE_{a3} = 0.26931 \)
となります.パラメータが3つあるので,n-3,としていることに注意です.
同じデータで,R,Kyplotで計算した結果は,ここ,にありますように,
Rでの近似を行ってみると,
プログラムは,
xx <- c(0,2,3,4,6,9)
yy <- c(11,5,3,2,1.5,1.1)
plot(xx,yy)
fm<-nls(yy~a0*exp(-a1*xx)+a2,start=c(a0=10,a1=0.5,a2=1),trace=TRUE)
summary(fm)
で,結果は,
| Parameters: | |||||
| Estimate | Std. Error | t value | Pr(>|t|) | ||
| a0 | 10.16402 | 0.37708 | 26.954 | 0.000112 | *** |
| a1 | 0.49456 | 0.04408 | 11.219 | 0.001518 | ** |
| a2 | 0.88393 | 0.26931 | 3.282 | 0.046348 | * |
となり,Kyplotにおいても,
| 推定値 | 標準誤差(SE) | |
| A1 | 10.16401 | 0.377081 |
| A2 | 0.494562 | 0.044083 |
| A3 | 0.883926 | 0.269308 |
と一致した結果となります.
わざわざ,Labview,を使わずに,R,を使えばいいんじゃない?,と言われそうですが,
Labviewでプログラム → 結果をcsvで出力 → Rで解析
という手間なく,一つのプログラムで完結できるのはやはり便利ですね.選択肢が広がることはよいことです.