フーリエ級数展開-12
ここで,三角関数を用いて解いた矩形波を複素数表示で解いてみましょう.
・矩形波
矩形波,
\( \Large \left\{ \begin{array}{c} \hspace{10pt} -1 \hspace{20pt} ( \pi \leq x < 0) \\ \hspace{20pt} 1 \hspace{20pt} (0 \leq x < \pi) \end{array} \right. \)
の場合を考えます.
フーリエ級数展開は,
\( \Large \displaystyle f(x) = \sum_{n= - \infty}^{ \infty} C_{n} \cdot e^{i \frac{ n \pi}{L}x } \)
\( \Large \displaystyle C_n = \frac{1}{2L} \int_{ - L}^{ L} f(x) \ \displaystyle e^{- i \frac{ n \pi}{L}x } \ dx \)
となり,積分範囲から,L=π,となるので,
\( \Large \displaystyle f(x) = \sum_{n= - \infty}^{ \infty} C_{n} \cdot e^{i n x } \)
\( \Large \displaystyle C_n = \frac{1}{2 \pi } \int_{ - \pi}^{ \pi} f(x) \ \displaystyle e^{- i n x} \ dx \)
となります.
n=0,の場合は,
\( \Large \displaystyle C_0 = \frac{1}{2 \pi } \int_{ - \pi}^{ \pi} f(x) \ dx
= \frac{1}{2 \pi } \left\{ \int_{ - \pi}^{ 0} (-1) \ dx + \int_{0}^{ \pi} 1 \ dx \right\} \)
\( \Large \displaystyle
= \frac{1}{2 \pi } \left\{ -\left[ x \right]_{- \pi}^0 + \left[ x \right]_0^{ \pi} \right\}
=
\frac{1}{2 \pi } ( - \pi + \pi) = 0 \)
n≠0,の場合は,
\( \Large \displaystyle C_n = \frac{1}{2 \pi } \int_{ - \pi}^{ \pi} f(x) \cdot e^{-i n x }\ dx
= \frac{1}{2 \pi } \left\{ \int_{ - \pi}^{ 0} (-1) \cdot e^{-i n x } \ dx + \int_{0}^{ \pi} 1 \cdot e^{-i n x }\ dx \right\} \)
\( \Large \displaystyle = \frac{1}{2 \pi } \left\{ \left[ \frac{-1}{-in} \cdot e^{-i n x } \right]_{- \pi}^0 + \left[ \frac{1}{-in} \cdot e^{-i n x } \right]_0^{ \pi} \right\} \)
\( \Large \displaystyle = \frac{1}{2 \pi } \left\{ \frac{1}{in} (1 - e^{i n \pi} ) - \frac{1}{in} ( e^{-i n \pi} - 1 )\right\} \)
\( \Large \displaystyle = \frac{1}{2 \pi in } \left\{ 2- e^{i n \pi} - e^{-i n \pi} \right\} \)
となります,ここで,
\( \Large \displaystyle e^{i n \pi} = cos ( n \pi) + i \ sin (n \pi) = cos ( n \pi) = (-1)^n \)
\( \Large \displaystyle e^{-i n \pi} = cos ( n \pi) - i \ sin (n \pi) = cos ( n \pi) = (-1)^n \)
となりますので,
\( \Large \displaystyle C_n = \frac{1}{2 \pi in } \left\{ 2- e^{i n \pi} - e^{-i n \pi} \right\} = \frac{1}{ \pi in } \left\{ 1-(-1)^n \right\}\)
\( \Large = \left\{ \begin{array}{c} \hspace{10pt} \frac{2}{ \pi i n} \hspace{20pt} ( n = odd ) \\ \hspace{20pt} 0 \hspace{20pt} (n = even) \end{array} \right. \)
となります.
Σを分割して,
\( \Large \displaystyle f(x) = \sum_{n= - \infty}^{ \infty} C_{n} \cdot e^{i n x } = C_0 + \sum_{ n=-\infty}^{-1} C_{n} \cdot e^{i n x } + \sum_{n= 1}^{ \infty} C_{n} \cdot e^{i n x } \)
として,m = -n,と変換して,
\( \Large \displaystyle = C_0 + \sum_{ m=\infty}^{1} C_{-m} \cdot e^{-i m x } + \sum_{n= 1}^{ \infty} C_{n} \cdot e^{i n x } \)
Σの範囲の順番は逆でもいいので,
\( \Large \displaystyle = C_0 + \sum_{m=1}^{ \infty} C_{-m} \cdot e^{-i m x } + \sum_{n= 1}^{ \infty} C_{n} \cdot e^{i n x } \)
記号を書き換えて,
\( \Large \displaystyle = C_0 + \sum_{n=1}^{ \infty} C_{-n} \cdot e^{-i n x } + \sum_{n= 1}^{ \infty} C_{n} \cdot e^{i n x } \)
Σをまとめて,
\( \Large \displaystyle = C_0 + \sum_{n=1}^{ \infty} ( C_{-n} \cdot e^{-i n x } + C_{n} \cdot e^{i n x }) \)
今回の計算では,nが偶数の場合は0,C0=0,となるので,
\( \Large \displaystyle f(x) = \sum_{n=1, odd}^{ \infty} ( C_{-n} \cdot e^{-i n x } + C_{n} \cdot e^{i n x }) \)
となります.第一項,第二項はそれぞれ,オイラーの公式から,
\( \Large \displaystyle C_{n} \cdot e^{i n x } = \frac{2}{ \pi i n} \{ cos (nx) + i \ sin (nx) \} \)
\( \Large \displaystyle C_{-n} \cdot e^{-i n x } = -\frac{2}{ \pi i n} \{ cos (nx) - i \ sin (nx) \} \)
となるので,
\( \Large \displaystyle C_{n} \cdot e^{i n x } + C_{-n} \cdot e^{-i n x } = \frac{2}{ \pi i n} \left[ \{ cos (nx) + i \ sin (nx) \} - \{cos (nx) - i \ sin (nx) \} \right] \)
\( \Large \displaystyle = \frac{4}{ \pi n} \left[ \ sin (nx) \right] \)
となりますので,
\( \Large \displaystyle f(x) = \sum_{n=1, odd}^{ \infty} ( C_{-n} \cdot e^{-i n x } + C_{n} \cdot e^{i n x }) \)
\( \Large \displaystyle= \sum_{n=1, odd}^{ \infty} \frac{4}{ \pi} \left[ \frac{ sin (nx)}{n} \right] \)
\( \Large \displaystyle= \frac{4}{ \pi} \left( sin \ x + \frac{1}{3} sin \ 3x + \frac{1}{5} sin \ 5x + ........... \right) \)

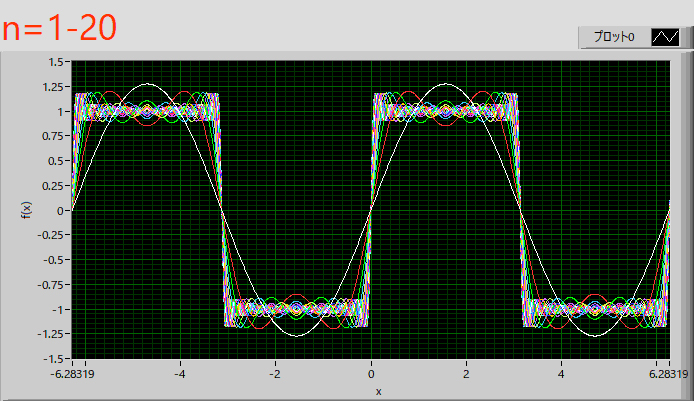
と,三角関数の場合,と同じ結果となります.
三角関数の場合と同様に,振幅,周期を変えてみるとどうなるでしょう?