フーリエ級数展開-13
ここで,三角関数を用いて解いた矩形波を複素数表示で解いてみましょう.
・矩形波
矩形波,
\( \Large \left\{ \begin{array}{c} \hspace{10pt} -1 \hspace{20pt} (\color{red}{-1} \leq x < 0) \\ \hspace{20pt} \color{red}{2} \hspace{20pt} (0 \leq x < \color{red}{1}) \end{array} \right. \)
の場合を考えます.
フーリエ級数展開は,
\( \Large \displaystyle f(x) = \sum_{n= - \infty}^{ \infty} C_{n} \cdot e^{i \frac{ n \pi}{L}x } \)
\( \Large \displaystyle C_n = \frac{1}{2L} \int_{ - L}^{ L} f(x) \ \displaystyle e^{- i \frac{ n \pi}{L}x } \ dx \)
となり,積分範囲から,L=1,となるので,
\( \Large \displaystyle f(x) = \sum_{n= - \infty}^{ \infty} C_{n} \cdot e^{i n \color{red}{\pi} x } \)
\( \Large \displaystyle C_n = \frac{1}{\color{red}{2} } \int_{ \color{red}{- 1}}^{ \color{red}{1}} f(x) \ \displaystyle e^{- i n \color{red}{\pi} x} \ dx \)
となります.
n=0,の場合は,
\( \Large \displaystyle C_0 = \frac{1}{2 } \int_{ - 1}^{ 1} f(x) \ dx
= \frac{1}{2 } \left\{ \int_{ - 1}^{ 0} (-1) \ dx + \int_{0}^{ 1} 2 \ dx \right\} \)
\( \Large \displaystyle
= \frac{1}{2 } \left\{ -\left[ x \right]_{- 1}^0 + \left[ 2x \right]_0^{ 1} \right\}
=
\frac{1}{2 } ( - 1 + 2) = \frac{1}{2} \)
n≠0,の場合は,
\( \Large \displaystyle C_n = \frac{1}{2 } \int_{ - 1}^{ 1} f(x) \cdot e^{-i n \pi x }\ dx
= \frac{1}{2 } \left\{ \int_{ - 1}^{ 0} (-1) \cdot e^{-i n \pi x } \ dx + \int_{0}^{ 1} 2 \ e^{-i n \pi x }\ dx \right\} \)
\( \Large \displaystyle = \frac{1}{2 } \left\{ \left[ \frac{-1}{-in \pi} \cdot e^{-i n \pi x } \right]_{- 1}^0 + \left[ \frac{2}{-in \pi } \cdot e^{-i n \pi x } \right]_0^{ 1} \right\} \)
\( \Large \displaystyle = \frac{1}{2 } \left\{ \frac{1}{in \pi} (1 - e^{i n \pi} ) - \frac{2}{in \pi } ( e^{-i n \pi} - 1 )\right\} \)
\( \Large \displaystyle = \frac{1}{2 \pi in } \left\{ 3- e^{i n \pi} - 2 e^{-i n \pi} \right\} \)
となります,ここで,
\( \Large \displaystyle e^{i n \pi} = cos ( n \pi) + i \ sin (n \pi) = cos ( n \pi) = (-1)^n \)
\( \Large \displaystyle e^{-i n \pi} = cos ( n \pi) - i \ sin (n \pi) = cos ( n \pi) = (-1)^n \)
となりますので,
\( \Large \displaystyle C_n = \frac{1}{2 \pi in } \left\{ 2- e^{i n \pi} - 2 e^{-i n \pi} \right\} = \frac{1}{ 2 \pi in } \left\{ 3-(-1)^n - 2 (-1)^n \right\}\)
\( \Large = \left\{ \begin{array}{c} \hspace{10pt} \frac{3}{ \pi i n} \hspace{20pt} ( n = odd ) \\ \hspace{20pt} 0 \hspace{20pt} (n = even) \end{array} \right. \)
となります.
Σを分割して,
\( \Large \displaystyle f(x) = \sum_{n= - \infty}^{ \infty} C_{n} \cdot e^{i n x } = C_0 + \sum_{ n=-\infty}^{-1} C_{n} \cdot e^{i n x } + \sum_{n= 1}^{ \infty} C_{n} \cdot e^{i n x } \)
として,m = -n,と変換して,
\( \Large \displaystyle = C_0 + \sum_{ m=\infty}^{1} C_{-m} \cdot e^{-i m x } + \sum_{n= 1}^{ \infty} C_{n} \cdot e^{i n x } \)
Σの範囲の順番は逆でもいいので,
\( \Large \displaystyle = C_0 + \sum_{m=1}^{ \infty} C_{-m} \cdot e^{-i m x } + \sum_{n= 1}^{ \infty} C_{n} \cdot e^{i n x } \)
記号を書き換えて,
\( \Large \displaystyle = C_0 + \sum_{n=1}^{ \infty} C_{-n} \cdot e^{-i n x } + \sum_{n= 1}^{ \infty} C_{n} \cdot e^{i n x } \)
Σをまとめて,
\( \Large \displaystyle = C_0 + \sum_{n=1}^{ \infty} ( C_{-n} \cdot e^{-i n x } + C_{n} \cdot e^{i n x }) \)
今回の計算では,nが偶数の場合は0,C0=0,となるので,
\( \Large \displaystyle f(x) = \sum_{n=1, odd}^{ \infty} ( C_{-n} \cdot e^{-i n x } + C_{n} \cdot e^{i n x }) \)
となります.第一項,第二項はそれぞれ,オイラーの公式から,
\( \Large \displaystyle C_{n} \cdot e^{i n x } = \frac{3}{ \pi i n} \{ cos (nx) + i \ sin (nx) \} \)
\( \Large \displaystyle C_{-n} \cdot e^{-i n x } = -\frac{3}{ \pi i n} \{ cos (nx) - i \ sin (nx) \} \)
となるので,
\( \Large \displaystyle C_{n} \cdot e^{i n x } + C_{-n} \cdot e^{-i n x } = \frac{3}{ \pi i n} \left[ \{ cos (nx) + i \ sin (nx) \} - \{cos (nx) - i \ sin (nx) \} \right] \)
\( \Large \displaystyle = \frac{6}{ \pi n} \left[ \ sin (nx) \right] \)
となりますので,
\( \Large \displaystyle f(x) = C_0 + \sum_{n=1, odd}^{ \infty} ( C_{-n} \cdot e^{-i n x } + C_{n} \cdot e^{i n x }) \)
\( \Large \displaystyle= \frac{1}{2} + \sum_{n=1, odd}^{ \infty} \frac{4}{ \pi} \left[ \frac{ sin (nx)}{n} \right] \)
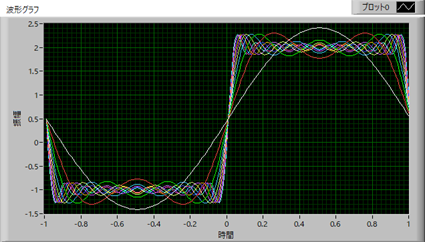
\( \Large \displaystyle= \color{red}{\frac{1}{2}} +\color{red}{\frac{6}{ \pi}} \left( sin \ x + \frac{1}{3} sin \ 3x + \frac{1}{5} sin \ 5x + ........... \right) \)

と,三角関数の場合,と同じ結果となります.
次は,三角波です.