アロステリックモデル再考-02

つぎに，n=3，の場合について考えていきましょう

n=3，の場合

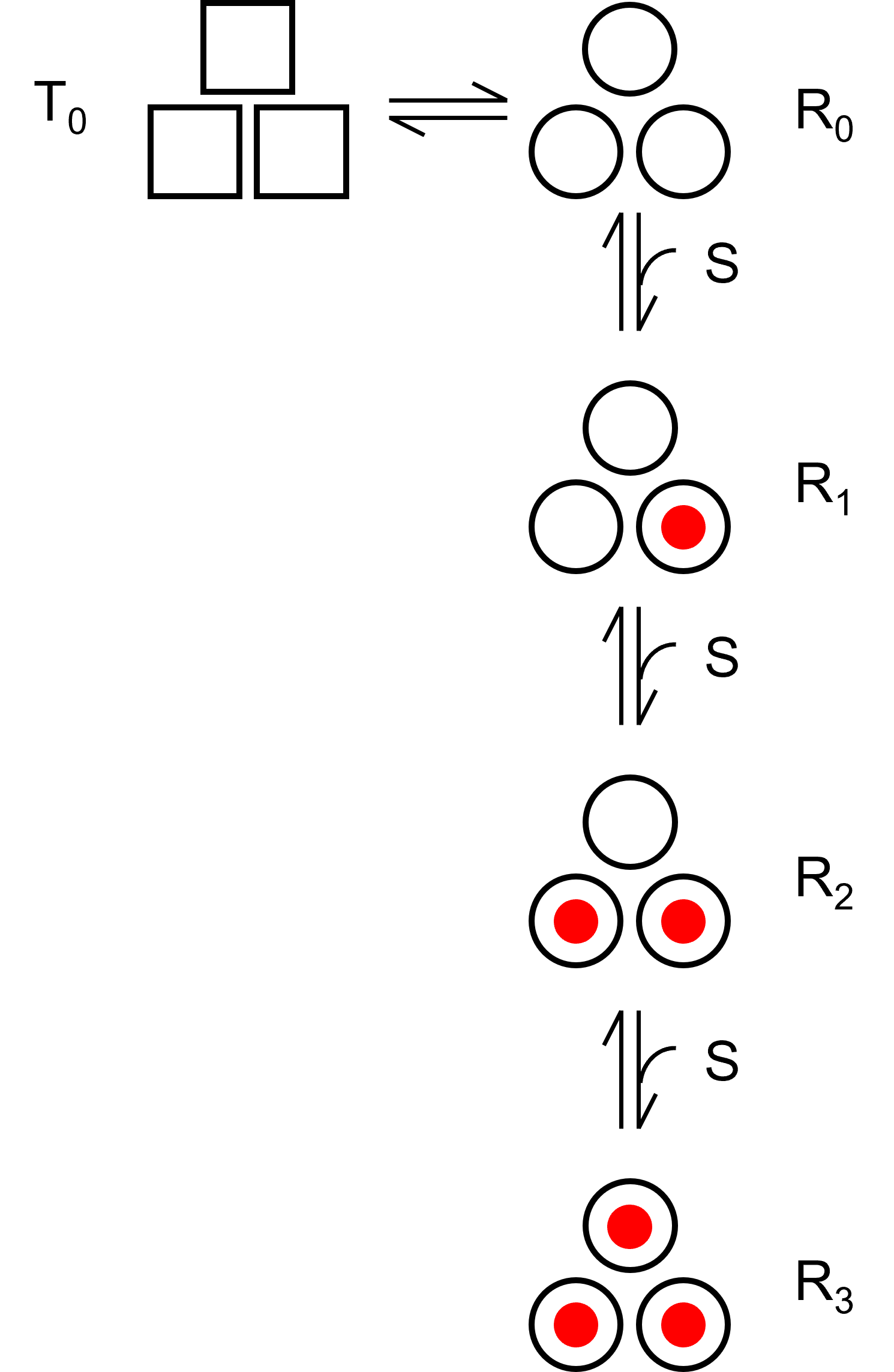
まずはT状態とR状態を遷移するモデルを考え，基質SはR状態のみに結合すると考えましょう．

また，モデルには3つの結合サイトがあるとします．

TとR

TとRは平衡状態にあり，その割合Lは，

\( \Large L= \frac{T_0}{R_0} \)

と書けます．

解離定数，K_R

ここで，R状態の基質Sに対する解離定数，K_Rは，

\( \Large K_R= \frac{3 R_0 S}{R_1} = \frac{ 2 R_1 S}{2 R_2} = \frac{ R_1 S}{3 R_2}\)

となります．それぞれの分子・分母に数字ががついている理由は，
　R₀には３つの可能な結合サイトがあり，解離するのは１つのみなので，R₀とRと₁の平衡では３と１
　R₁には2つの可能な結合サイトがあり，解離するのは2つの可能性があるので，R₁とRと₂の平衡では2と2
　R₂には1つの可能な結合サイトのみであり，解離するのは3つの可能性があるので，R₂とRと₃の平衡では1と3
となるからです．

R₁，R₂，R₃

R₁，R₂，R₃は，

\( \Large R_1 = \frac{3 S}{K_R} R_0 \)

\( \Large R_2 = \frac{S}{K_R} R_1 = \frac{3 S^2}{ K_R^2} R_0 \)

\( \Large R_3 = \frac{S}{3 K_R} R_2 = \frac{S^3}{ K_R^3} R_0 \)

５状態の結合サイトの総数

５状態の結合サイトの総数は，各状態に３つずつ結合サイトがありますので，

\( \Large \begin{eqnarray} \Large 3( T_0 + R_0 + R_1 +R_2 + R_3 ) &=& 3(L R_0 + R_0 + \frac{3 S}{K_R} R_0 + \frac{3 S^2}{ K_R^2} + \frac{S^3}{ K_R^3} R_0) \\
&=& 3 R_0 \left[ L + 1 + \frac{3 S}{K_R} R_0 + \frac{3 S^2}{ K_R^2} + \frac{S^3}{ K_R^3} R_0 \right] \\
&=& 3 R_0 \left[ L + \left( 1 + \frac{ S}{K_R} \right)^3 \right] \\
\end{eqnarray} \)

となります．

基質Sが結合している数

基質Sが結合している数は，

\( \Large \begin{eqnarray} \Large R_1 +2 R_2 + 3 R_3 &=& \frac{3 S}{K_R} R_0 + 2 \frac{3 S^2}{K_R^2} R_0 + 3 \frac{ S^2}{K_R^2} R_0\\
&=& 3 R_0 \left[ \frac{ S}{K_R} + 2 \frac{S^2}{K_R^2} + \frac{ S^2}{K_R^2} \right] \\
&=& 3 R_0 \frac{ S}{K_R} \left( 1 + \frac{S}{K_R} \right)^2 \\
\end{eqnarray} \)

基質飽和度

基質飽和度，Yは，

\( \Large \begin{eqnarray} Y &=& \frac{R_1 +2 R_2 + 3 R_3 }{3( T_0 + R_0 + R_1 +R_2 + R_3)} \\
&=& \frac{ 3 R_0 \frac{ S}{K_R} \left( 1 + \frac{S}{K_R} \right)^2 }{3 R_0 \left[ L + \left( 1 + \frac{ S}{K_R} \right)^3 \right])} \\
&=& \frac{ \frac{ S}{K_R} \left( 1 + \frac{S}{K_R} \right)^2}{ L + \left( 1 + \frac{ S}{K_R} \right)^3 } \\
\end{eqnarray} \)

となります．

次のページに，n，の場合についての計算を行います．