アロステリックモデル再考-01

アロステリックモデルに関しては，以前にもここで説明しましたが，再度検討してみたいと思います．

さらには，MWCモデルにまで拡張していきたいと思います．

まずは前回と同様に，ストライヤーの生化学，を参考にして計算していこうと思います．

n=2，の場合

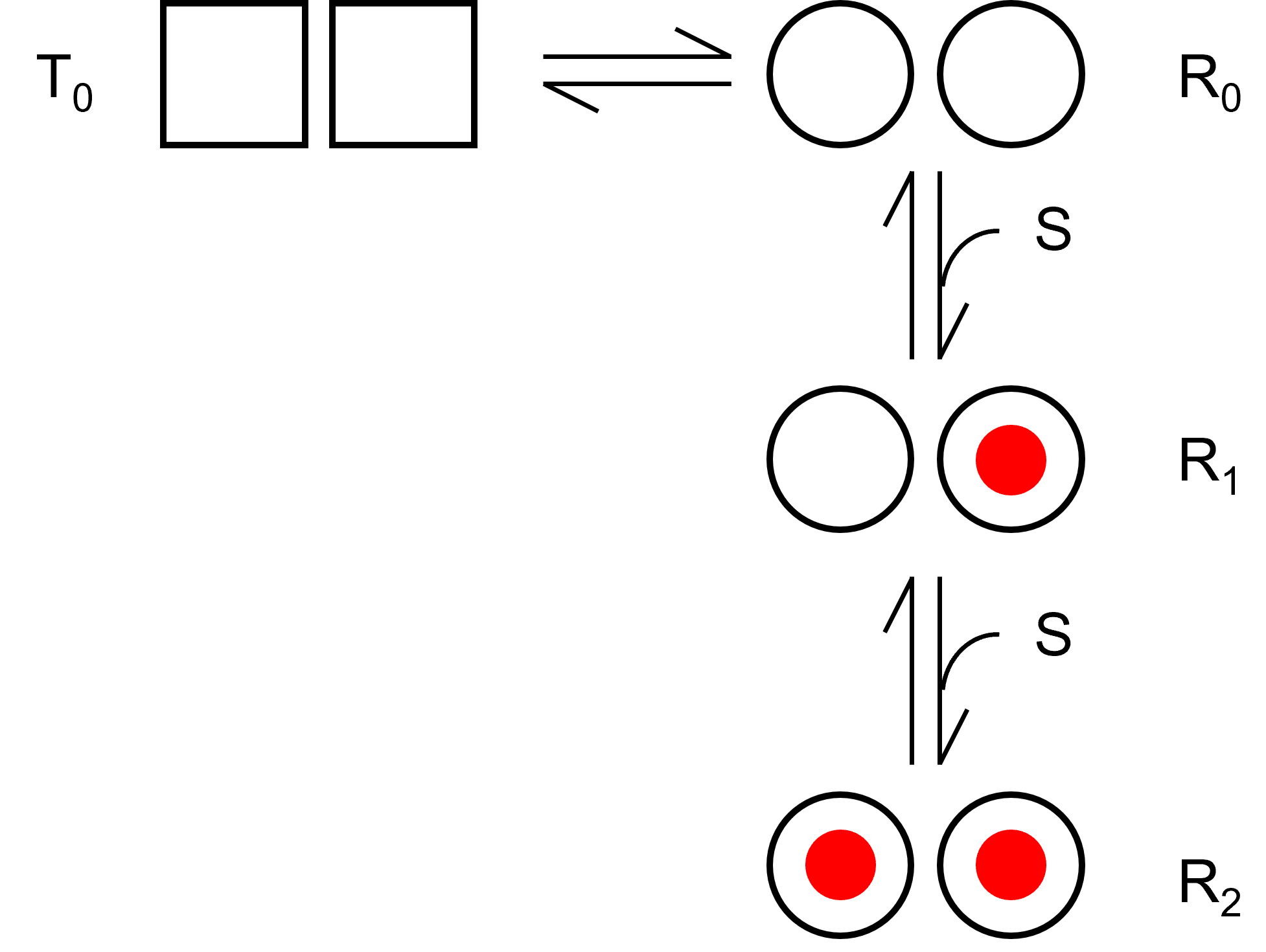
まずはT状態とR状態を遷移するモデルを考え，基質SはR状態のみに結合すると考えましょう．

また，モデルには2つの結合サイトがあるとします．

TとR

TとRは平衡状態にあり，その割合Lは，

\( \Large L= \frac{T_0}{R_0} \)

と書けます．

解離定数，K_R

ここで，R状態の基質Sに対する解離定数，K_Rは，

\( \Large K_R= \frac{2 R_0 S}{R_1} = \frac{ R_1 S}{2 R_2}\)

となります．それぞれの分子・分母に２がついている理由は，R₁には２状態があるためです，つまり，

\( \Large \ce{R_{10} <=>C[k_-][k_+ S ] R_0 <=>C[k_+ S ][k_-] R_{01}} \)

となるので，

\( \Large \frac{d R_0}{dt} = -2 k_+ R_0 S + k_- ( R_{10} + R_{01}) =-2 k_+ R_0 S + k_- S R_1 \)

平衡状態では，

\( \Large 2 k_+ R_0 S = k_- R_1 \)

\( \Large K_R = \frac{k_-}{k_+} = \frac{2 R_0 S}{ R_1} \)

同様に，

\( \Large \ce{R_{10} <=>C[k_+ S][k_- ] R_2 <=>C[k_- ][k_+ S] R_{01}} \)

となるので，

\( \Large \frac{d R_2}{dt} = -2 k_- R_2S + k_+ S( R_{10} + R_{01}) =-2 k_- R_2 S + k_+ R_1 \)

平衡状態では，

\( \Large 2 k_- R_2 = k_+ S R_1 \)

\( \Large K_R = \frac{k_-}{k_+} = \frac{ R_1 S}{2 R_2} \)

となります．

R₁，R₂

R₁，R₂は，

\( \Large R_1 = \frac{2 S}{K_R} R_0 \)

\( \Large R_2 = \frac{S}{2 K_R} R_1 = \frac{S^2}{K_R^2} R_0 \)

４状態の結合サイトの総数

４状態の結合サイトの総数は，各状態に２つずつ結合サイトがありますので，

\( \Large \begin{eqnarray} \Large 2( T_0 + R_0 + R_1 +R_2) &=& 2(L R_0 + R_0 + \frac{2 S}{K_R} R_0 + \frac{S^2}{K_R^2} R_0) \\
&=& 2 R_0 \left[ L + 1 + \frac{2 S}{K_R} + \frac{S^2}{K_R^2} \right] \\
&=& 2 R_0 \left[ L + \left( 1 + \frac{ S}{K_R} \right)^2 \right] \\
\end{eqnarray} \)

となります．

基質Sが結合している数

基質Sが結合している数は，

\( \Large \begin{eqnarray} \Large R_1 +2 R_2 &=& \frac{2 S}{K_R} R_0 + 2 \frac{S^2}{K_R^2} R_0 \\
&=& 2 R_0 \left[ \frac{ S}{K_R} + \frac{S^2}{K_R^2} \right] \\
&=& 2 R_0 \frac{ S}{K_R} \left[ 1 + \frac{S}{K_R} \right] \\
\end{eqnarray} \)

基質飽和度

基質飽和度，Yは，

\( \Large \begin{eqnarray} Y &=& \frac{R_1 +2 R_2}{2( T_0 + R_0 + R_1 +R_2)} \\
&=& \frac{ 2 R_0 \frac{ S}{K_R} \left( 1 + \frac{S}{K_R} \right)}{2 R_0 \left[ L + \left( 1 + \frac{ S}{K_R} \right)^2 \right])} \\
&=& \frac{ \frac{ S}{K_R} \left( 1 + \frac{S}{K_R} \right)}{ L + \left( 1 + \frac{ S}{K_R} \right)^2 } \\
\end{eqnarray} \)

となります．

ここで，気になる点は，
　解離定数，K，は単純な二状態でなくても上記のように書けるの？
という疑問がわきました．そこで，計算してみました（ここです）

次のページに，n=3，の場合についての計算を行います．