吸光-02

ランベルト・ベールの法則の導き出し方

ランベルト・ベールの法則の導き出し方はこの，サイト，を参考にさせていただきました．ありがとうございます．

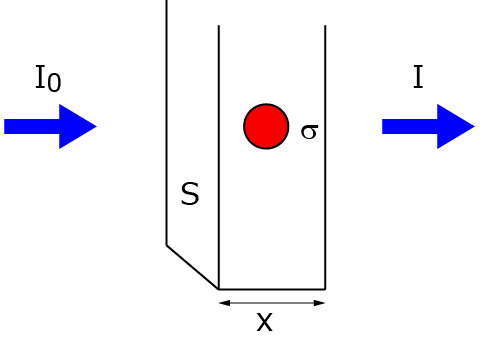
まず，試料中に断面積σの分子が一つ存在する場合を考えましょう．
強度I0の光が面積S，厚みｘに照射されると考えます．断面積σの分子は光を完全に遮断します．また，

　S >> σ

とします．

透過する光強度は，

\(\Large I(x) = I_0 \ \left(1- \frac{\sigma}{S} \right) \)

となります．

では，N分子存在するときにはどうなるのでしょう？

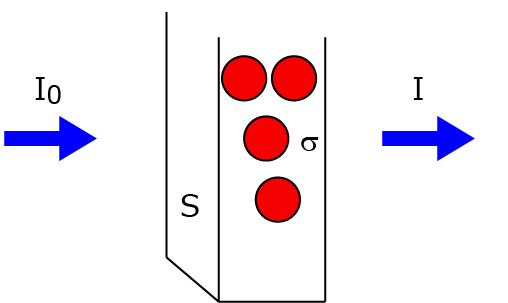
この場合の透過強度，I(x)，は，

\(\Large I(x) = I_0 \ \left(1- \frac{\sigma}{S} \right)^N \)

となります．注意すべき点はN倍ではなく，N乗，です．

なぜ，N乗，なのでしょうか？　以下の図を見るとよくわかります．．

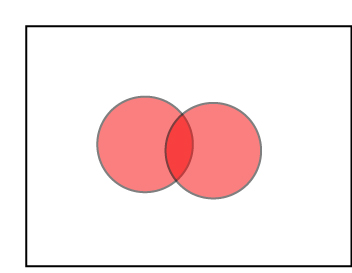
小学校のときに習った，ベン図，ですね．

全体を１，赤円を０．１として考えていきましょう．

１つの円に入る確率が0.1となります．

２つの円に入る確率は0.1✕0.1＝0.01，となります（濃い赤い円）．

したがって，赤い部分に入る確率は，0.1 + 0.1 - 0.01✕0.01 =0.19

よって赤い部分に入らない確率は，1 - 0.19 = 0.81 = 0.9²

となります．

さてこの対数をとると，

\(\Large ln \frac{ I(x)}{I_0} = ln \left[ \left(1- \frac{\sigma}{S} \right)^N \right] \)

となります．Nと濃度との関係は，

\(\Large c = \frac{N}{S \cdot x} \)

となるので，

\(\Large N = S \cdot c \cdot x \)

となり，

\(\Large ln \frac{ I(x)}{I_0} = S \cdot c \cdot x \ \ ln \left(1- \frac{\sigma}{S} \right) \)

となります．

次ページに近似を加えて式を展開していきましょう．