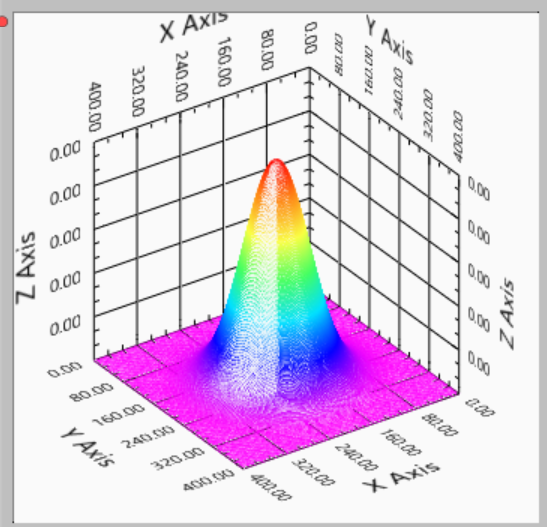
2次元ガウシアン画像の理論計算-01

2次元ガウシアンの積分

蛍光顕微鏡で蛍光像の観察を行う際に，重要なポイントは，

　強度を計算したい

という局面が頻繁に出てきます．

その際に，どこまでを積分範囲にするか，という点でいつも悩みます．
と言うのも，ガウス分布なので，いつまでたっても（無限大になっても）強度は理論上０にならないからです．

そこで，一般的に使われるのが，
　σ，もしくは２σまでの積分
です．

一次元の場合は，具体的な計算は，ここ，に記してあるように，
　　σ　：　68％
　２σ　：　95％
と，２σまでの範囲ならほぼよいと考えてもいいことになります．

では，二次元の場合はどのように計算すればよいでしょう？

この数式は，

\( \Large Z= \frac{1}{ \sqrt{2 \ \pi \ \sigma_x^2}} e^{- \frac{(x-x_0)^2}{2 \ \sigma_x^2}} \times \frac{1}{ \sqrt{2 \ \pi \ \sigma_y^2}} e^{- \frac{(y-y_0)^2}{2 \ \sigma_y^2}}\)

で表すことができます．簡単に，原点を０としてx,yのσを等しいとすれば，

\( \Large Z= \frac{1}{ 2 \ \pi \ \sigma^2} e^{- \frac{x^2+y^2}{2 \ \sigma^2}} \)

となります．

では，中心からσまでの範囲での積分はどうなるのでしょうか？

私も勘違いしましたが，

\( \Large \displaystyle \int_{- \sigma}^{\sigma} \int_{- \sigma}^{\sigma} \frac{1}{ 2 \ \pi \ \sigma^2} e^{- \frac{x^2+y^2}{2 \ \sigma^2}} dx dy
= \int_{- \sigma}^{\sigma} \frac{1}{ \sqrt{2 \ \pi \ \sigma^2}} e^{- \frac{x^2}{2 \ \sigma^2}} dx \times \int_{- \sigma}^{\sigma} \frac{1}{ \sqrt{2 \ \pi \ \sigma^2}} e^{- \frac{y^2}{2 \ \sigma^2}} dy \)

としてはいけません！

このままだと，正方形のエリア，を積分してしまうことになるからです．

半径σ内の計算ですので，ｘとｙは独立ではないのです．

その関係は，半径ｒの場合，

\( \Large x^2 + y^2 = r^2 \)

\( \Large x = \sqrt{r^2 - y^2} \)

となるので，

\( \Large \displaystyle \int_{- \sigma}^{\sigma} \int_{- \sigma}^{\sigma} \frac{1}{ 2 \ \pi \ \sigma^2} e^{- \frac{x^2+y^2}{2 \ \sigma^2}} dx dy
= \displaystyle \int_{- \sigma}^{\sigma} \int_{- \sqrt{\sigma^2-y^2}}^{\sqrt{\sigma^2-y^2}} \frac{1}{ 2 \ \pi \ \sigma^2} e^{- \frac{x^2+y^2}{2 \ \sigma^2}} dx dy \)

となるのが正解です．

しかし！，この最初の定積分で誤差関数を含む式となり，さらにそれを積分となるはとてもややこしいですね．．．．

ですので，極座標で計算してみることにします．

次ページをご覧ください．