RLC回路におけるステップ応答-05

RL回路からの内部抵抗測定

つぎに，RL回路について考えていきましょう．

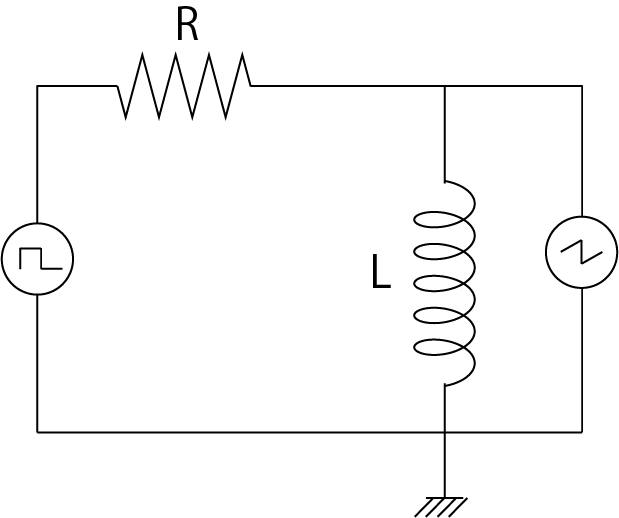
対象となる回路は，以下に示すものです．

となります．

RL回路

RL回路は，Cがないので，

\( \Large \ RI + L \frac{dI}{dt} = V_0 \)

で表すことができます

したがって，上の式を書き直すと，

\( \Large \ L \ I' + R \ I = V_0 \)

と，一階の微分方程式となります．この微分方程式を解きます．

定数変化法を使うので，まずは定数が0で計算します．

\( \Large \ L I' + R \ I= 0 \)

\( \Large \ I' = -\frac{R}{L} I \)

\( \Large \ I = A e^{-\frac{R}{L} t} \)

ここで定数Aを時間の関数として，

\( \Large \ I = A(t) \ e^{-\frac{R}{L} t} \)

再度Iを微分すると，

\( \Large \ I' = A'(t) \ e^{-\frac{R}{L} t} - \frac{R}{L}A(t) \ e^{-\frac{R}{L} t} \)

元の式に代入すると，

\( \Large \ L A'(t) \ e^{-\frac{R}{L} t} - L \frac{R}{L}A(t) \ e^{-\frac{R}{L} t} + R \ A(t) \ e^{-\frac{R}{L} t} = V_0 \)

左辺，第二項と第三項は打ち消し合うので，

\( \Large \ L A'(t) \ e^{-\frac{R}{L} t} = V_0 \)

\( \Large \ A'(t) = \frac{V_0}{L} e^{\frac{R}{L} t} \)

\( \Large \ A(t) = \frac{L}{R} \frac{V_0}{L} e^{\frac{R}{L} t} + B =\frac{V_0}{R} \ e^{\frac{R}{L} t} + B \)

Iの式に代入すると，

\( \Large \ I = \left( \frac{V_0}{R} \ e^{\frac{R}{L} t} + B \right) \ e^{-\frac{R}{L} t} =\frac{V_0}{R}+ B \ e^{-\frac{R}{L} t} \)

初期条件として，t=0，でq=0，とすると，

\( \Large \ 0 =\frac{V_0}{R} + B \)

\( \Large \ B = - \frac{V_0}{R} \)

\( \Large \ I =\frac{V_0}{R} \left( 1 - \ e^{-\frac{R}{L} t} \right) \)

電圧の求め方

RL回路において，

\( \Large \ L \ I' + R \ I = V_L + V_R = V_0 \)

となるので，

\( \Large \begin{eqnarray} V_L
&=& L I' \\
&=& L \ \frac{V_0}{R} \frac{R}{L}\ e^{-\frac{R}{L} t} \\
&=& V_0\ e^{-\frac{R}{L} t} \\
&=& V_0\ e^{-\frac{t}{\tau} } \\
\end{eqnarray} \)

\( \Large \tau = \frac{L}{R} \)

となります．

内部抵抗

内部抵抗があるので（波形発生器，コイルに），

\( \Large \ \tau = \frac{L}{ R + R_{sys} } \)

となりますので，

\( \Large \ R = \frac{L}{\tau} - R_{sys} \)

とRと1/τとの関係を求めれば，

　傾き：L

　切片：-R_sys

となります．

また，ここ，にあるように，対数で考えると，

\( \Large \ \tau = \frac{\tau}{R + R_{sys}} \)

\( \Large \ ln \ \tau= -ln (R + R_{sys}) + ln \ L \)

とR_sysを設定すれば，

　傾き：-1

　切片：ln \ L

となります．

次に実験結果となります．