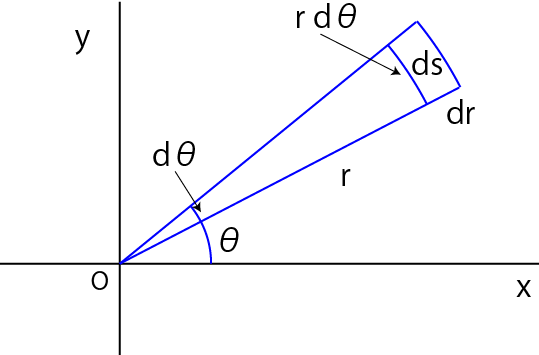
極座標変換

上図のような配置を考えます．

\(\Large x = r \ cos \theta, \quad y = r \ sin \theta \)

微小領域dsを考えると，

\(\Large \begin{eqnarray} ds
&=& \pi (r + dr)^2 \times \frac{d \theta}{2 \pi} - \pi r^2 \times \frac{d \theta}{2 \pi} \\
&=& \left[ (r + dr)^2- r^2 \right] \times \frac{d \theta}{2} \\
&=& \left[ 2 r dr- (dr)^2 \right] \times \frac{d \theta}{2} \\
&=& r \ dr \ d \theta + \frac{1}{2} (dr)^2 d \theta \\
\end{eqnarray}　\)

となります．

第二項は無視できるので，

\(\Large ds = dx \ dy = \rho \ d \rho \ d \phi \)

となります