矩形開口からの回折-22

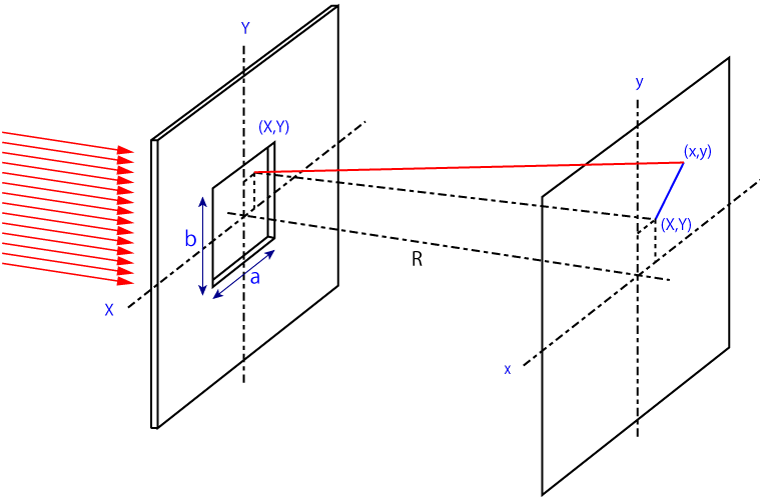
矩形開口

開口部が四角い場合を考えましょう．

この場合は簡単です，二重積分を別々に計算すればいいのです．

\(\Large \begin{eqnarray} E
&=& \frac{E_0 e^{i ( \omega t - k R )}}{z} \int_{Aperture} e^{ ik \frac{(Xx+Yy)}{R}} ds \\
&=& \frac{E_0 e^{i ( \omega t - k R )}}{z} \int_{-a/2}^{a/2} e^{ik \frac{Xx}{R}} dX \int_{-b/2}^{a/2} e^{ik \frac{Yy}{R}} dY \\
\end{eqnarray}　\)

となり，この二重積分の部分を計算すればよいのです．

今回は強度の絶対値は考慮せず形状のみ考えますし，二つの積分は同じなので，

\(\Large e^{ik \frac{Xx}{R}} dX \)

のみの計算でいいことがわかります．

\(\Large \begin{eqnarray} \int_{-a/2}^{a/2} e^{ik \frac{Xx}{R}} dX
&=& \frac{R}{iKx} \left[ exp \left[ ik \frac{Xx}{R} \right] \right]_{-a/2}^{a/2} \\
&=& \frac{R}{iKx} \left[ exp \left[ ik \frac{xa}{2R} \right] - exp \left[- ik \frac{xa}{2R} \right]\right] \\
\end{eqnarray}　\)

\(\Large \alpha \equiv \frac{kax}{2R} \)

とすれば，

\(\Large = a \frac{[exp[i \alpha]-exp[-i \alpha]]}{2 i \alpha} \)

となります．オイラーの公式より，

\(\Large = a \frac{sin \alpha}{\alpha} \)

となります．同様に，

\(\Large \beta \equiv \frac{kby}{2R} \)

とすれば，

\(\Large = b \frac{[exp[i \beta]-exp[-i \beta]]}{2 i \beta} \)

となり，

\(\Large = b \frac{sin \beta}{\beta} \)

となります．強度は二乗平均となるので，

\(\Large I \propto \left( \frac{sin \alpha}{\alpha} \right)^2 \left( \frac{sin \beta}{\beta} \right)^2 \)

となります．

この結果は，一個のスリットの回折-01の結果と（当然ながら）一致します．