回折-11
一個のスリットの回折-01
スリットが1個の場合はどうなるのでしょう?
これも回折現象が起こります.
一つの開口の各点からの光が干渉し合って,回折現象を起こします.

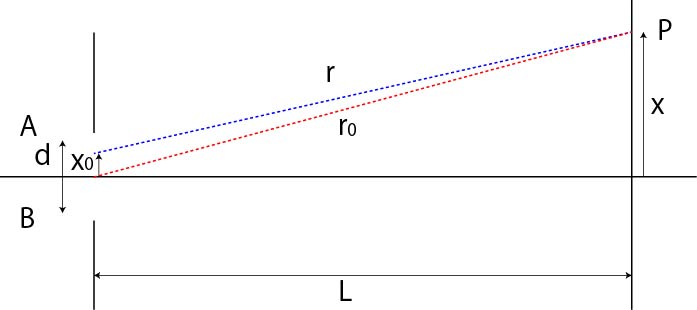
開口幅,d,の各点から発せられた光の干渉光は,距離Lだけ離れたスクリーン上に投影されます.
距離xの位置のP点での光強度をスリット全域で積分すればよいので,
\(\Large r = \sqrt{L^2 + (x-x_0)^2} \)
となります.ここで,
\(\Large r_0 = \sqrt{L^2 + x^2} \)
とすると,
\(\Large \begin{eqnarray}
r &=& \sqrt{L^2 + x^2 - 2xx_0 + x_0^2} \\
&=&
\sqrt{r_0^2 - 2xx_0 + x_0^2} \\
&=&
r_0 \sqrt{1+\frac{ -2xx_0 + x_0^2}{r_0^2}}
\end{eqnarray} \)
となります.ここで,(1+x)aのテイラー展開を使えば(計算は,ここ),
\(\Large \begin{eqnarray}
r &=& r_0 \left[ 1+\frac{1}{2}\frac{ -2xx_0 + x_0^2}{r_0^2}
\right] \\
&=& r_0 \left[ 1-\frac{xx_0}{r_0^2}+\frac{1}{2}\frac{ x_0^2}{r_0^2}
\right] \end{eqnarray} \)
となります,ここまでを,フレネル近似,と呼びます.
さらに,近似を行います.第3項を無視すると,
\(\Large r \simeq r_0 \left[ 1-\frac{xx_0}{r_0^2} \right] \)
となります,ここまでを,フラウンフォーファ近似,と呼びます.
では,次に積分を行ってみましょう.