二次元軌跡から,移動速度,角度変化を求める方法-02
前ページにあるように,
・移動距離
\(\Large \Delta r = \displaystyle \sqrt{ (x_{t + \Delta t} - x_t)^2 + (y_{t + \Delta t} - y_t)^2} \)
・角度
\(\Large \theta = \displaystyle tan^{-1} \left( \frac{\vec{a} \times \vec{b}}{\vec{a} \cdot \vec{b}}\right) \)
でした. この角度が右回りか,左回りかは,分母の内積は+の値ですから,分子の外積によるものと思われます.
外積は,
\(\Large\vec{a} \times \vec{b} = a_x \ b_y - a_y \ b_x \)
となります.ベクトルa,bの角度は(第一象限で考えると),
\(\Large\theta_a = \frac{a_y}{a_x} \)
\(\Large\theta_b = \frac{b_y}{b_x} \)
となり,もし反時計回りなら,
\(\Large\theta_b > \theta_a\)
となり,
\(\Large \frac{b_y}{b_x} > \frac{a_y}{a_x}\)
\(\Large a_x \ b_y - a_y \ b_x > 0 \)
となるため,外積が,
+ : 反時計回り
- : 時計回り
となります.
では,角度変化の計算を具体的な数値を元に計算していきましょう.
・具体的な手順
具体的な手順としては,
1. 時系列上の各点の座標から,一つ前の座標からの差分を計算し,それぞれのベクトルを求める.
2. 一つ前のベクトルとの内積,外積を計算し,移動距離,角度を計算する
でした.実際に単純なデータから手順を見ていきましょう.
まずは,簡単なデータ列を作成します.
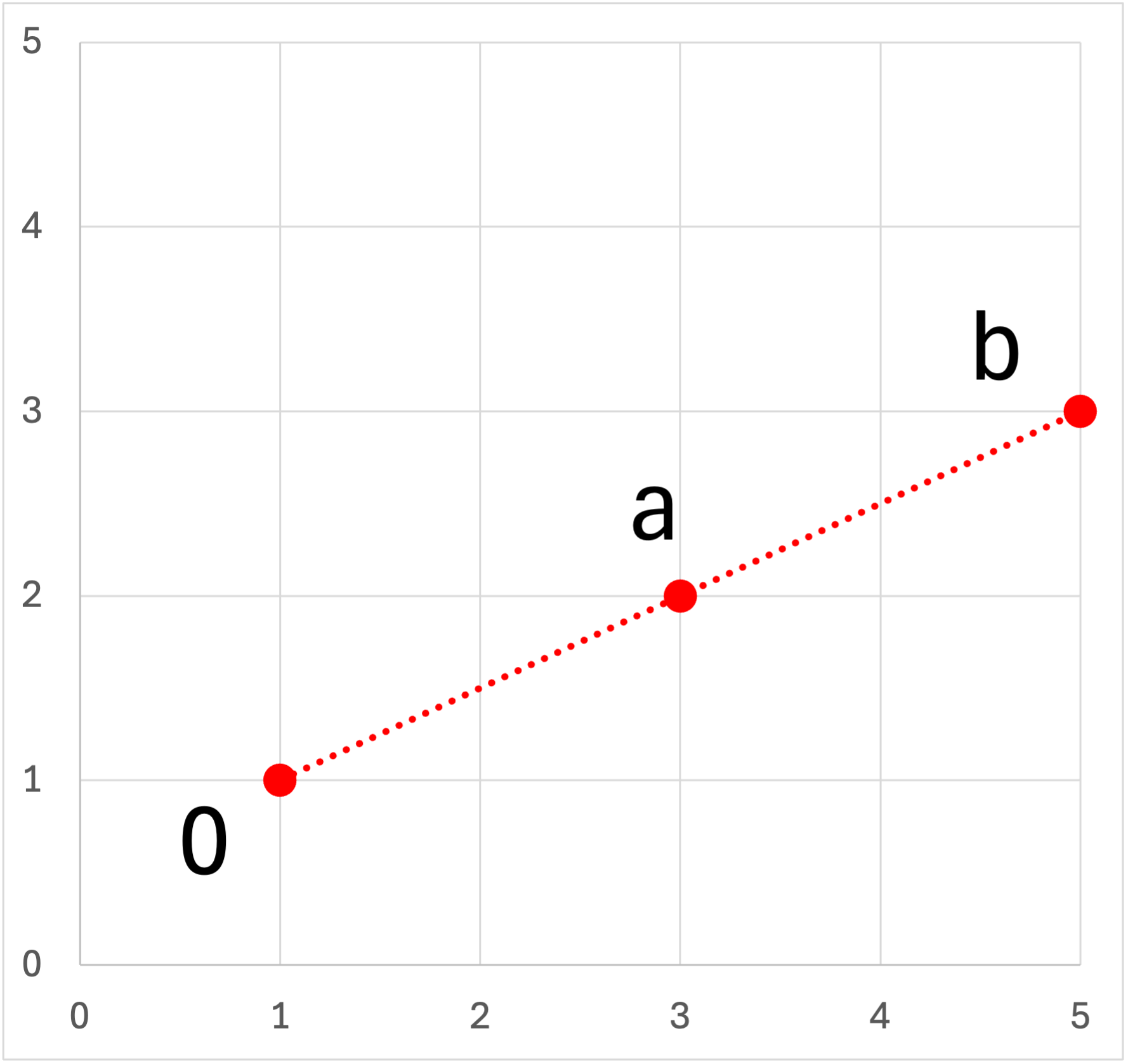
・角度変化:0
| x | y | Δx | Δy |
| 1 | 1 | ||
| 3 | 2 | 2 | 1 |
| 5 | 3 | 2 | 1 |

一直線ですので,角度変化は0のはず,計算してみましょう.
\(\Large\vec{a} \cdot \vec{b} = a_x \ b_x - a_y \ b_y = 2 \times 2 + 1 \times 1 = 5 \)
\(\Large\vec{a} \times \vec{b} = a_x \ b_y - a_y \ b_x = 2 \times 1 - 2 \times 1 = 0\)
\(\Large \theta = \displaystyle tan^{-1} \left( \frac{\vec{a} \times \vec{b}}{\vec{a} \cdot \vec{b}}\right) = tan^{-1} \left( \frac{0}{5}\right) = 0\)
となり,角度変化は0であることがわかります.
・角度変化:+
| x | y | Δx | Δy |
| 1 | 1 | ||
| 3 | 2 | 2 | 1 |
| 4 | 5 | 1 | 3 |
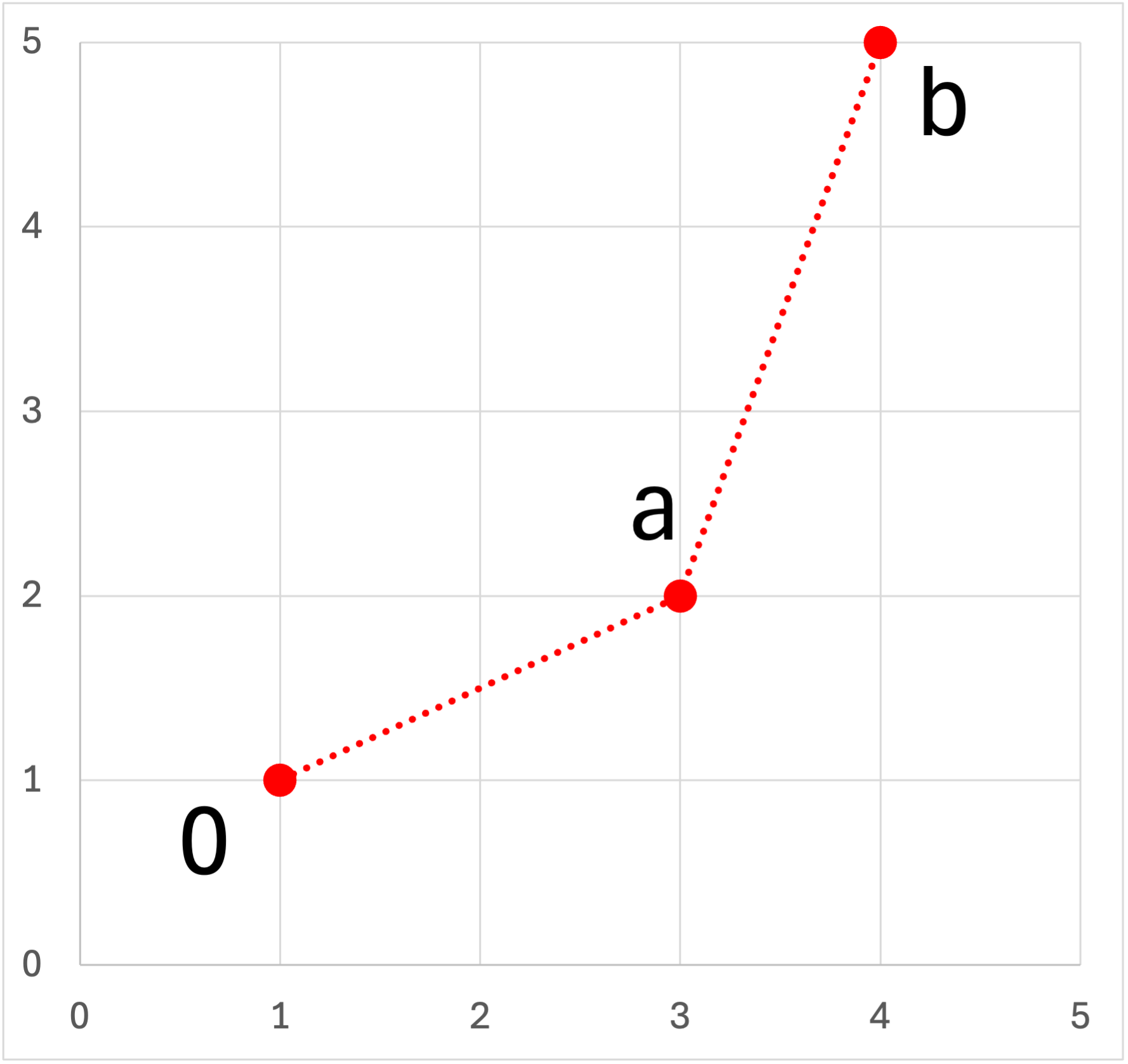
計算してみましょう.
\(\Large\vec{a} \cdot \vec{b} = a_x \ b_x - a_y \ b_y = 2 \times 1 + 1 \times 3 = 5 \)
\(\Large\vec{a} \times \vec{b} = a_x \ b_y - a_y \ b_x = 2 \times 3 - 1 \times 1 = 5\)
\(\Large \theta = \displaystyle tan^{-1} \left( \frac{\vec{a} \times \vec{b}}{\vec{a} \cdot \vec{b}}\right) = tan^{-1} \left( \frac{5}{5}\right) = 45^o\)
となり,角度変化は45度であり,θb > θaであるので外積がプラスであることがわかります.
・角度変化:-
| x | y | Δx | Δy |
| 1 | 1 | ||
| 3 | 2 | 2 | 1 |
| 5 | 1 | 2 |
-1 |
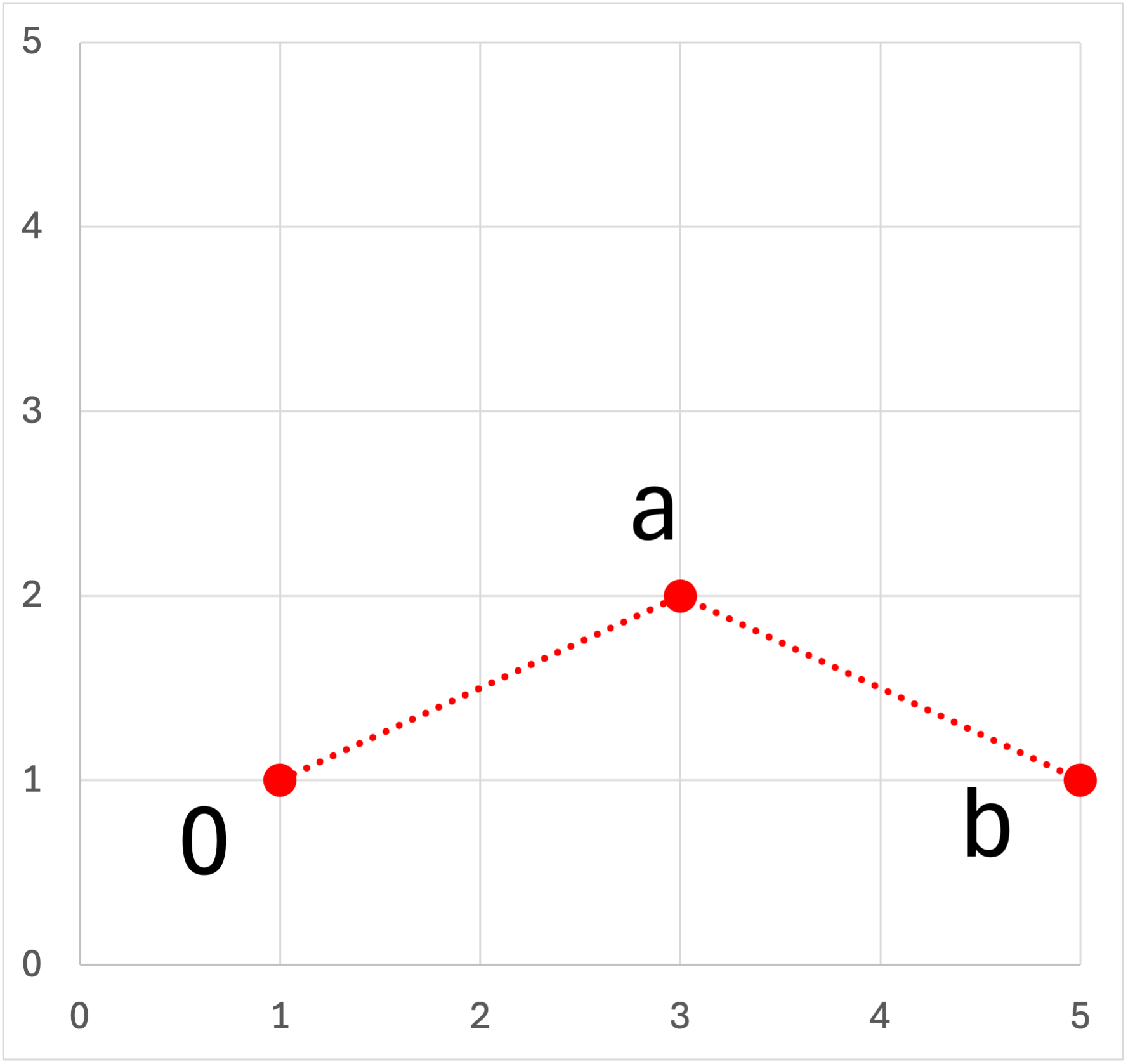
計算してみましょう.
\(\Large\vec{a} \cdot \vec{b} = a_x \ b_x - a_y \ b_y = 2 \times 2 + 1 \times (-1) = 3 \)
\(\Large\vec{a} \times \vec{b} = a_x \ b_y - a_y \ b_x = 2 \times (-1) - 1 \times 2 = -4\)
\(\Large \theta = \displaystyle tan^{-1} \left( \frac{\vec{a} \times \vec{b}}{\vec{a} \cdot \vec{b}}\right) = tan^{-1} \left( \frac{-4}{3}\right) = -53.1^o\)
となり,角度変化は-53度であり,θb < θaであるので外積がマイナスであることがわかります.