二次元軌跡から，移動速度，角度変化を求める方法

大腸菌の遊泳，など二次元映像から移動速度，角度変化を求める，ことがよくあります．

その際の数学を検討しましょう．

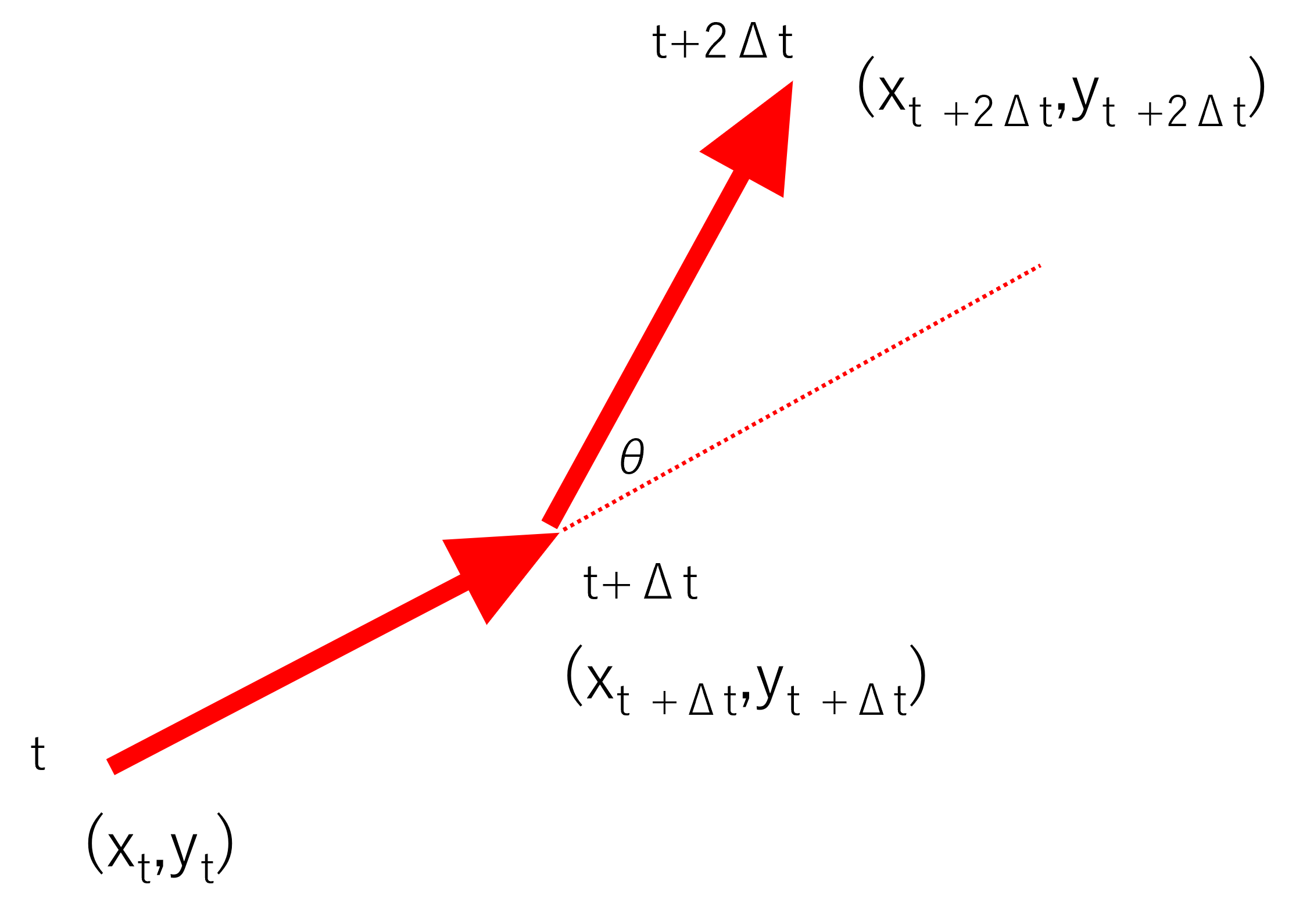
図のように，ｔ，ｔ＋Δｔ，ｔ＋２Δｔ，という3点を考えていきます．

・移動距離

これは簡単で，

\( \Large \displaystyle \Delta r_1 = \sqrt{(x_{t+ \Delta t } - x_{t })^2 + (y_{t+ \Delta t } - y_{t })^2} \)

\( \Large \displaystyle \Delta r_2 = \sqrt{(x_{t+ 2 \Delta t } - x_{t+ \Delta t })^2 + (y_{t+2 \Delta t } - y_{t+ \Delta t })^2} \)

を計算すればいいだけです．

・角度変化

これがいろいろ厄介ですが，理解してみるとそんなに難しくはなかったです．

メインは，内積，です．内積は，二次元空間においては，

\( \Large \displaystyle \vec{a} \cdot \vec{b} = |\vec{a}| | \vec{b}| \ cos \ \theta = a_x \ b_x + a_y \ b_y \)

からθを計算することができます．

\( \Large \displaystyle \theta = cos^{-1} \left[ \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| | \vec{b}|} \right] \)

しかし，このままでは角度がわかっても，どちらの向きかはわかりません．

そこで，登場するのが，外積，です．

外積は，二次元空間においては，

\( \Large \displaystyle \vec{a} \times \vec{b} = |\vec{a}| | \vec{b}| \sin \ \theta = a_x \ b_y - a_y \ b_x \)

となります．したがって，

\( \Large \displaystyle tan \ \theta = \frac{ sin \ \theta}{ cos \ \theta } = \frac{\vec{a} \times \vec{b}}{|\vec{a}| | \vec{b}|} \frac{|\vec{a}| | \vec{b}|}{{ \vec{a} \cdot \vec{b}}} = \frac{\vec{a} \times \vec{b}}{ \vec{a} \cdot \vec{b}} \)

\( \Large \displaystyle \theta = tan^{-1} \left( \frac{\vec{a} \times \vec{b}}{ \vec{a} \cdot \vec{b}} \right) \)

で計算できます．

象限を厳密に考えると，

\( \Large \displaystyle \theta = atan2 \left( \vec{a} \times \vec{b}, \ \vec{a} \cdot \vec{b} \right) \)

の計算を行えばいいことになります．

実際の計算では，それぞれの位置をベクトルで表さなければいけないので，

\( \Large \displaystyle t \ : \hspace{40 pt} a_x = x_{t + \Delta t} - x_t, \hspace{40 pt} a_y = y_{t + \Delta t} -y_t \)

\( \Large \displaystyle t + \Delta t : \hspace{4 pt} \ b_x = x_{t + 2 \Delta t} - x_{t + \Delta t}, \hspace{20 pt} b_y = y_{t + 2 \Delta t} -y_{t + \Delta t} \)

を計算してからとなります．

ただし，ややこしいのが，ここ，に記したように，atan2．．．．使うソフトによって使い方が異なります．

atan2(x,y)　：　エクセル，GoogleSheets, Numbers, Kyplot

atan2(y,x)　：　Python, R

などです．エクセル互換性のあるソフトは，エクセルに準じているようです．

なぜこんな混乱があるかは，よく知りませんが，それぞれのソフトに適した使い方をしていかなくてはならないですね．