逐次反応における自己相関関数について-02
r回の逐次反応が起こる確率
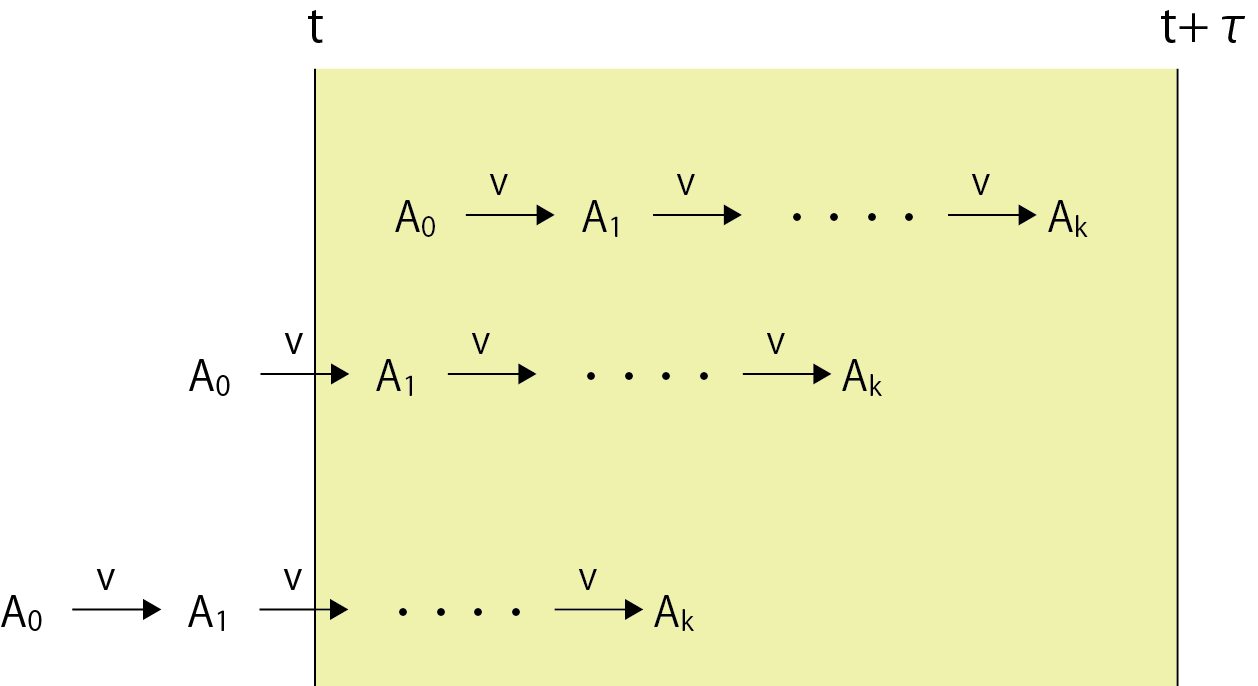
次に,t秒からt+τ秒の間にr回の逐次反応が起こる確率を求めましょう. つまり, 反応の回数がr回起こらないと反応が起こらないので,
0 |
~ |
r-1 |
逐次反応は起こらない |
r |
~ |
2r-1 |
1回逐次反応が起こる |
2r |
~ |
3r-1 |
2回逐次反応が起こる |
となります.
ただし,この計算は,τ秒前にイベントが起こっていない場合です.
すでに観測しているτ秒の間より以前に逐次反応が進行中かもしれない.

なので, すでに1回各反応が起こっている場合には,
0 |
~ |
r-2 |
逐次反応は起こらない |
r-1 |
~ |
2r-2 |
1回逐次反応が起こる |
2r-1 |
~ |
3r-2 |
2回逐次反応が起こる |
となるのです.同様に,すでに2回,すでに3回,といろいろな場合が想定されます.
ですので,この平均を取ればよいわけです.
これをまとめると,1回も起こらない確率(mはこの逐次反応が起こる確率)は,
\(\Large prob \left[ m=0 \ in \ interval (t, t + \tau) \right] =
\begin{bmatrix} & (P_0 + P_1 + \cdots + P_{r-1}) \\
+ & (P_0 + P_1 + \cdots + P_{r-2}) \\
+ & \cdots \\
+ & P_0 \\ \end{bmatrix} \)
となります.書き換えると,
\(\Large prob \left[ m=0 \ in \ interval (t, t + \tau) \right] = \frac{1}{r} \displaystyle \sum_{ i = 0 }^{ r } \displaystyle \sum_{ j = 0 }^{ r-i} P_j \)
となります.
同様に,1回起こる確率は,
\(\Large prob \left[ m=1 \ in \ interval (t, t + \tau) \right] =
\begin{bmatrix} & (P_r + P_{r+1} + \cdots + P_{2r-1}) \\
+ & (P_{r-1} + P_r + \cdots + P_{2r-2}) \\
+ & \cdots \\
+ & P_1 + P_2+ \cdots + P_r \\ \end{bmatrix} \)
となります.書き換えると,
\(\Large \hspace{ 210pt } = \frac{1}{r} \displaystyle \sum_{ i = 1 }^{ r } \displaystyle \sum_{ j = 1 }^{ r} P_{r-i+j} \)
となります.
同様に,2回起こる確率は,
\(\Large prob \left[ m=2 \ in \ interval (t, t + \tau) \right] =
\begin{bmatrix} & (P_{2r} + P_{2r+1} + \cdots + P_{3r-1}) \\
+ & (P_{2r-1} + P_{2r} + \cdots + P_{3r-2}) \\
+ & \cdots \\
+ & P_{r+1} + P_{r+2}+ \cdots + P_{2r} \\ \end{bmatrix} \)
となります.書き換えると,
\(\Large \hspace{ 210pt } = \frac{1}{r} \displaystyle \sum_{ i = 1 }^{ r } \displaystyle \sum_{ j = 1 }^{ r} P_{2r-i+j} \)
となります.
つまり,m回起こる確率(m=0を除く)は,
\(\Large prob \left[ m, \ m \ integer >0 \ in \ interval (t, t + \tau) \right] = \frac{1}{r} \displaystyle \sum_{ i = 1 }^{ r } \displaystyle \sum_{ j = 1 }^{ r} P_{rm-i+j} \)
と書くことができます.
次ページに,自己相関の導き出し方を計算していきましょう.