パワースペクトルの実際の作業内容-03

　縦軸が，”パワースペクトル密度(nm²/Hz)

という点を確かめておきましょう．

実際に，ここ，に記したように，

\(\Large \displaystyle <x^2> = \int_{- \infty}^{\infty} \Phi (\omega) \ d \omega \)

とパワースペクトルの全積分が分散値となります．したがって，横軸がHzならば，縦軸が
　分散÷Hz=nm²/Hz
となるわけです．

では，実際にそうなっているかパワースペクトルを作ってみて確認してみましょう．

まずは，おさらいから，実際の波形とフーリエ変換後の波形との関係を見ていきましょう．

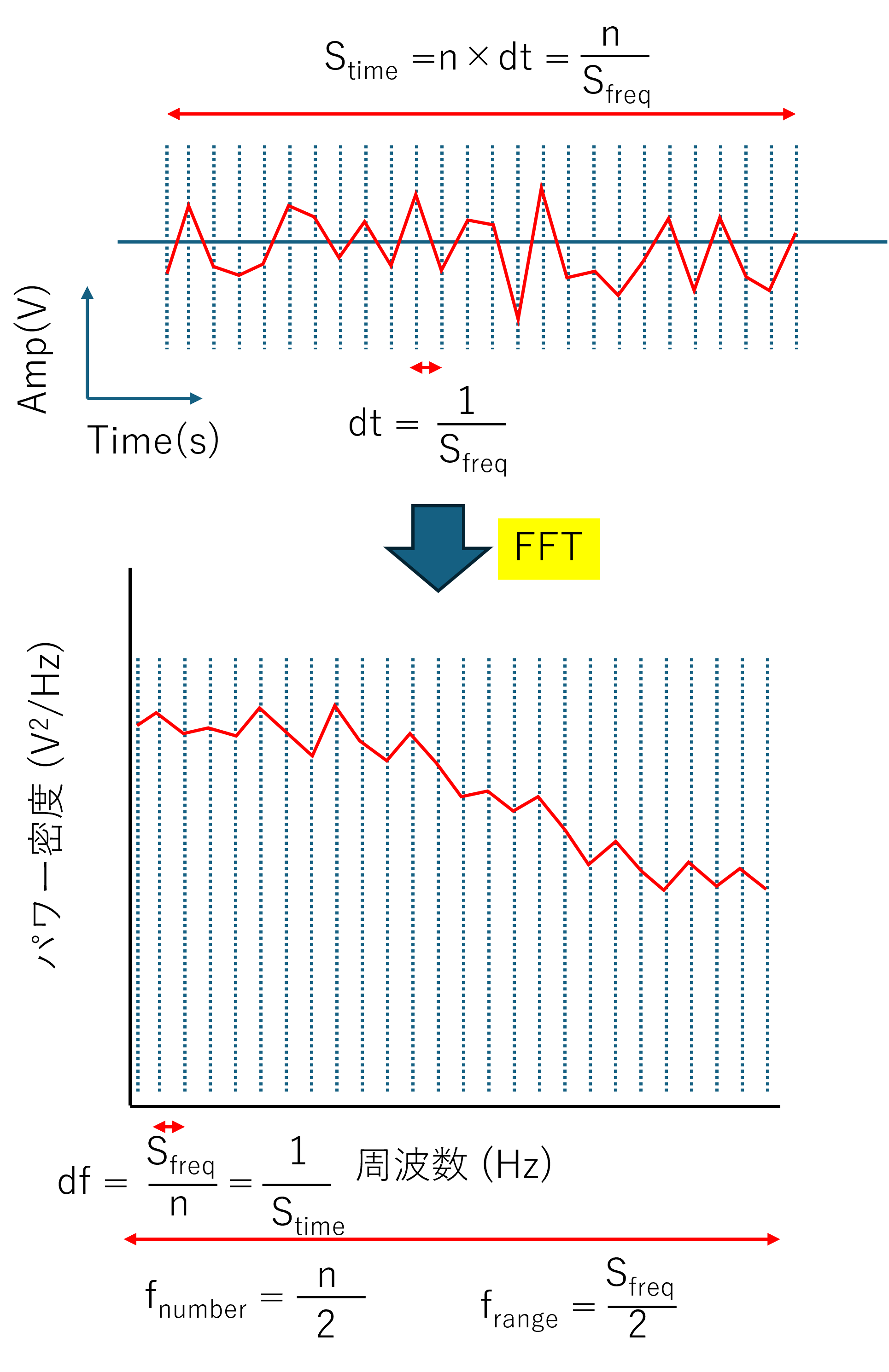
ここ，に示したように，下図にあるように，

　実際の波形の時間 (s)　　：　S_time
　サンプル周波数 (1/s)　　：　S_freq
　サンプル時間分解能 (s)　：　dt
　実際の波形の数　　　　　：　n

とすると，

\(\Large \displaystyle S_{time} = n \times dt = \frac{n}{S_{freq}} \)

の関係になります．これにフーリエ変換すると，

　フーリエ変換の横軸の最小単位 (Hz)　　　：　df
　フーリエ変換の横軸の数　　　　　　　　：　f_number
　フーリエ変換の横軸のレンジ（最大値）　： 　f_range

とすると，

\(\Large \displaystyle df = \frac{S_{freq}}{n} = \frac{1}{S_{time}}\)

\(\Large \displaystyle f_{number} = \frac{n}{2} \)

\(\Large \displaystyle f_{range} = \frac{S_{freq}}{2} \)

となります．

次ページから，実際にプログラムを作ってみましょう．