直線近似の求め方-01

まずは，直線近似の求め方を考えましょう．
エクセルで簡単に計算することができますが，ここは一つきちんと計算していきましょう．
まずは，以下のようなデータを考えます．

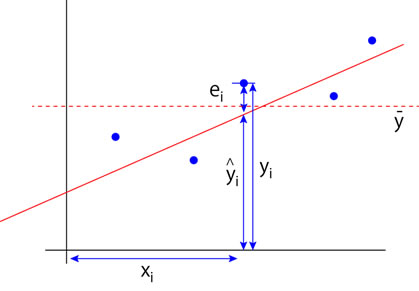
青いプロットがデータ，赤い線が直線近似，赤い点線がデータの平均値となります．

また，ここで，
xi, yi　；　各データ（N個）
\( \Large \displaystyle \hat{y }\)；回帰分析によるxiにおける推定値
\( \Large \displaystyle \bar{y }\)；yiの平均値
です．

この回帰直線は以下の式で表すことができます．

\( \Large \displaystyle \hat{y_i } = a x_i +b \)

この，a，ｂを求めるのが目的となります．
また各点における回帰分析による推定値と実測値との差は，

\( \Large \displaystyle e_i = y_i -\hat{y_i} =y_i - (a x_i +b) \)

となりますので，この差分，ei，の二乗の和が最小となる，a,bを求めればいいことになります．
つまり，

\( \Large \displaystyle \frac{ \partial }{ \partial a } \displaystyle \sum_{i=1}^n e_i =\frac{ \partial }{ \partial b } \displaystyle \sum_{i=1}^n e_i =0\)

を求めればいいのです．