化学平衡論

化学平衡論について，基質濃度と存在確率との関係について考えていきます．

一次の化学平衡

単純な一次の化学平衡において，

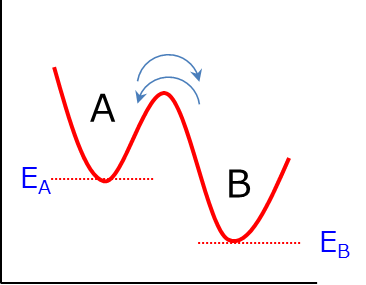
\( \Large \hspace{15 pt} \ce{A <=>C[ k_{AB} ][k_{BA}]B} \)

を考えます．A状態とB状態は平衡状態にあり，各々行き来しながらそれぞれの滞在割合は一定であると言えます．

それぞれのエネルギー状態は，E_A, E_Bである．ここで，E_A＞E_B，とします．

各状態の存在比がボルツマン分布に従うとして，それぞれの存在確率は，

\( \Large \displaystyle P_A \propto exp \left[ - \frac{E_A}{k_B T} \right] \)

\( \Large \displaystyle P_B \propto exp \left[ - \frac{E_B}{k_B T} \right] \)

その比は，

\( \Large \displaystyle \frac{P_A}{P_B} = exp \left[ - \frac{E_A - E_B}{k_B T} \right] = exp \left[ - \frac{\Delta E}{k_B T} \right]\)

となります．ここで，前提として，E_A＞E_B，なので，ΔE>0，となります．つまり，

\( \Large \displaystyle \frac{P_A}{P_B} < 1 \rightarrow P_A < P_B \)

となります．エネルギー状態が低いほうが存在確率が大きいのは納得できます．

この場合の平衡は，

\( \Large k_{BA} \cdot P_A = k_{AB} \cdot P_B \)

となるので，平衡定数Kを使って，

\( \Large K \equiv \frac{k_{BA}}{k_{AB}} = \frac{ P_B}{ P_A } \)

となります（平衡状態においてKの定義が上記でいいのか，その逆数がいいのかは，よく知らないです）

ここで，A， Bという二状態のみ考えているので，保存則より，

\( \Large P_A + P_B = 1\)

が成り立つので，

\( \Large \displaystyle P_A + \frac{P_A}{K} = 1\)

\( \Large \displaystyle P_A \left( 1+ \frac{1}{K} \right) = 1\)

\( \Large \displaystyle P_A =\frac{1}{1+K} = \frac{K}{1+K} \)

\( \Large \displaystyle P_B = \frac{1}{1+K} \)

が成り立ちます．

次に，基質が結合する反応を考えます．