RLC回路-04

\( \Large \left( \frac {R}{2L} \right) ^2 = \frac{1}{LC} \)

この場合には，

\( \Large x = e^{- \frac{R}{2L}t} \left[
A \ e^{ \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}} t }
+B \ e^{ - \sqrt{\left( \frac {R}{2L} \right) ^2 -\frac{1}{LC}}t}
\right] 　\)

において，平方根の中が0となりますので，簡単に，

\( \Large x = e^{- \frac{R}{2L} t} 　\)

となります．

これも一つの独立解ですが，もう一つの解を求める必要があります．

その詳細については，ここ，をご覧ください．

その解き方は，（ここ，を参考にしました）

\( \Large \frac{d^2 x}{dt^2} + \frac{R}{L} \frac{dx}{dt} +\frac{1}{LC} x =0 \)

において，\( \Large \left( \frac {R}{2L} \right) ^2 =\frac{1}{LC}　\)なので，

\( \Large \frac{d^2 x}{dt^2} + \frac{R}{L} \frac{dx}{dt} +\left( \frac{R}{2L} \right)^2 x =0 \)

を解くことになります．　

このとき，一つの解は，先に出た，

\( \Large x_1 = e^{- \frac{R}{2L} t} 　\)

となります．このxとは独立な解を見つける必要があります．それには，定数変化法が有効で，

\( \Large x_2 = C(t) \ x_1(t) = C(t) e^{- \frac{R}{2L} t} 　\)

これを先の式に代入します．

\( \Large \frac{d^2 x}{dt^2} + \frac{R}{L} \frac{dx}{dt} +\left( \frac{R}{2L} \right)^2 x =0 \)

\( \begin{eqnarray} && \left[ C''(t) x_1(t)+2C'(t) x'_1(t)+C(t) x_1''(t) \right] + \frac{R}{L} \left[ C'(t) x_1(t)+C(t) x'_1(t) \right] +\left( \frac{R}{2L} \right)^2 C(t) x_1(t) \\
&=& C(t) \left[ x_1''(t) + \frac{R}{L} x'_1(t) + \left( \frac{R}{2L} \right)^2 x_1(t) \right] + \left[ C''(t) x_1(t)+2C'(t) x'_1(t) + \frac{R}{L} C'(t) x_1(t) \right] \\
\end{eqnarray}　\)

となります．

第一項は先の微分方程式と一致するので，0となります．従って，

\( \Large C''(t) x_1(t)+2C'(t) x'_1(t) + \frac{R}{L} C'(t) x_1(t) =0 　\)

\( \Large x_1 = e^{- \frac{R}{2L} t} 　\)　なので，

\( \Large \begin{eqnarray}　&& C''(t) x_1(t)+2C'(t) x'_1(t) + \frac{R}{L} C'(t) x_1(t) \\
&=& C''(t) e^{- \frac{R}{2L} t}-2 \frac{R}{2L} C'(t) e^{- \frac{R}{2L} t} + \frac{R}{L} C'(t) e^{- \frac{R}{2L} t} \\
&=& C''(t) e^{- \frac{R}{2L} t} \\
&=& 0 \\
\end{eqnarray}　\)

つまり，

\( \Large C''(t) e^{- \frac{R}{2L} t} = 0　\)　

\( \Large C''(t) = 0　\)　

となります．

\( \Large C'(t) = D_2　\)

\( \Large C(t) = D_2 t + D_1　\)

となるので，

\( \Large x_2 = ( D_2 t + D_1 ) e^{- \frac{R}{2L} t }　\)

まとめると，

\( \Large \begin{eqnarray} x &=& x_1 +x_2 \\
&=& D_0 e^{- \frac{R}{2L} t } + ( D_2 t + D_1 ) e^{- \frac{R}{2L} t }　\\
&=& ( D_2 t + D ) e^{- \frac{R}{2L} t }　\\
\end{eqnarray}　\)

初期条件として

\( \Large t=0 \quad -> \quad x=1 \)

\( \Large t=0 \quad -> \quad x'=0 \)

とします．

・　\( \Large t=0 \quad -> \quad x=1 \)

\( \Large 1 = D　\)

・　\( \Large t=0 \quad -> \quad x'=0 \)

\( \Large x' = - \frac{R}{2L} ( D_2 t + D ) e^{- \frac{R}{2L} t }+ D_2 e^{- \frac{R}{2L} t }　　\)

\( \Large 0 = - \frac{R}{2L} \ D+ D_2 \)

\( \Large D_2 = \frac{R}{2L} \)

つまり，

\( \Large x = ( \frac{R}{2L} t + 1) e^{- \frac{R}{2L} t }　　\)

となります．

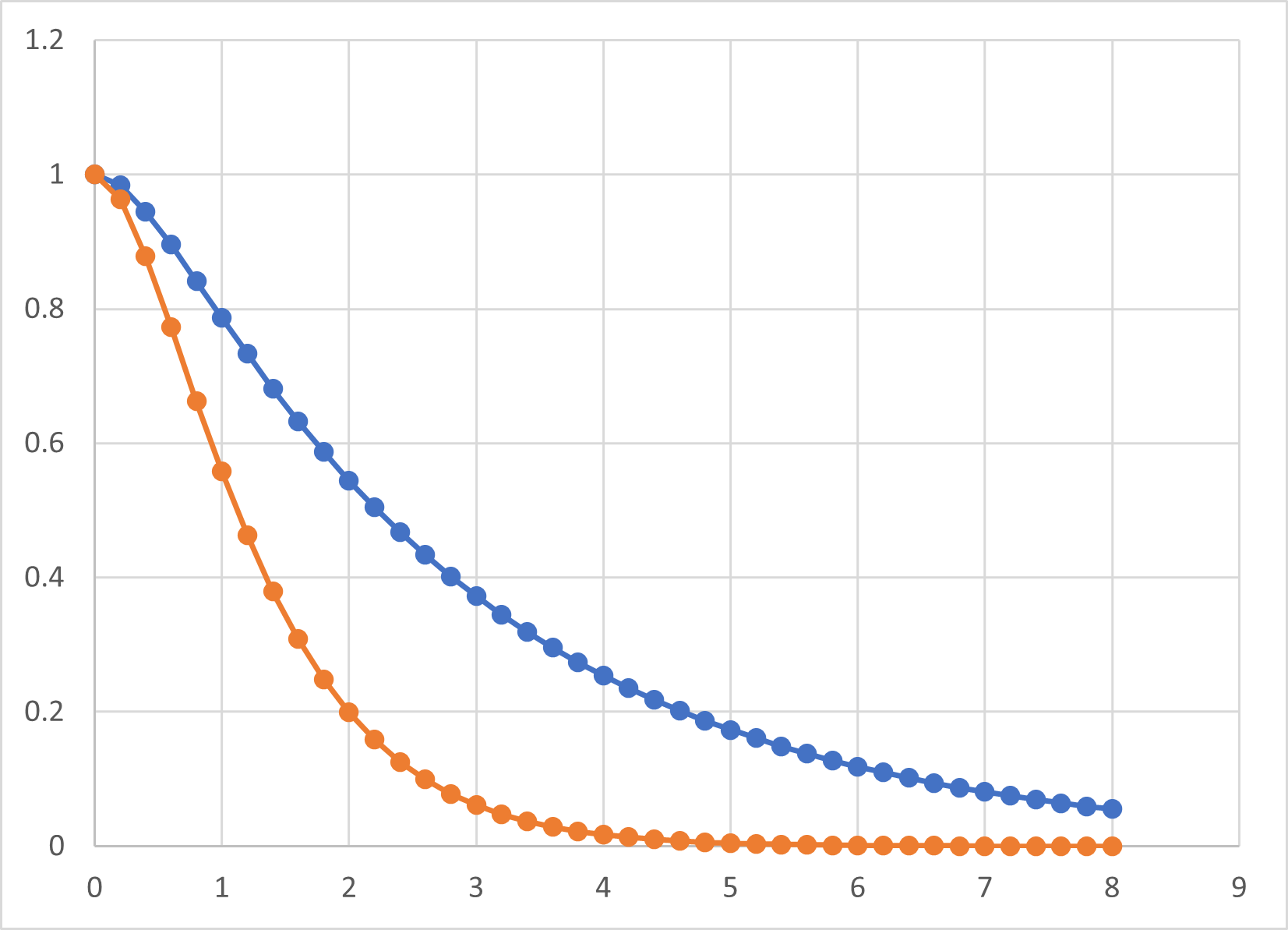
\( \Large \left( \frac {R}{2L} \right) ^2 > \frac{1}{LC} 　\) と\( \Large \left( \frac {R}{2L} \right) ^2 = \frac{1}{LC} 　\)とを比較してみると，

青：\( \Large \left( \frac {R}{2L} \right) ^2 > \frac{1}{LC} 　\)
オレンジ：\( \Large \left( \frac {R}{2L} \right) ^2 = \frac{1}{LC} 　\)

であり，臨界減衰が早く減衰することが分かります．