さて,遠心力,というと,バケツに水を入れてひもをつけてくるくる,というイメージがありますが,どのような力が働くかを考えてみましょう.
このサイト,を参考にしました.
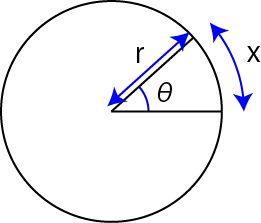
まずは,弧度法,から.
これは,角度をラジアンではかること,です.つまり,
一回転=360° → =2π
とすることです.何でそんなことをするかというと,
半径rの円の円周は2π
なので,
rθ=円弧の長さ
と簡単に描けるからです.

次は,角速度,です.
角速度の定義は,
単位時間あたりの回転角
で表すことができます.つまり,
\( \Large \displaystyle \omega = \frac{ \Delta \theta}{ \Delta t} \ [rad/s] \)
となります.
等速円運動の場合は,
\( \Large \displaystyle \omega = \frac{ \theta}{ t} \)
\( \Large \displaystyle \theta = \omega \cdot t \)
となります.
次に,円運動,について考えましょう.
まずは,
長さr,質量0の糸に結ばれた質量mの円運動
を考えましょう.
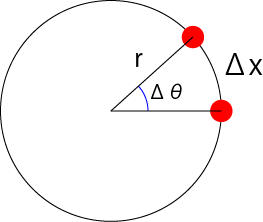
微小時間Δt[s]の間に,Δθ[rad]だけ回転した場合,の移動距離Δx[m]は,
\( \Large \displaystyle \Delta x = r \cdot \Delta \theta \)
速度v[m/s]は,
\( \Large \displaystyle v = \frac{ \Delta x}{ \Delta t} = \frac{ r \cdot \Delta \theta}{ \Delta t} = r \cdot \omega \)
となる.
このとき,速度ベクトルは円の接線の方向になるので,
速度ベクトルは刻一刻と変化する=加速度が生じる
ことになります.また,そのときの,
加速度ベクトルは速度ベクトルに直交する
ことになります.
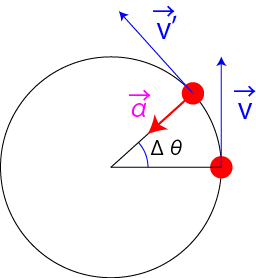
速度ベクトルの変化をわかりやすくするために,図を以下のように書き直しましょう.
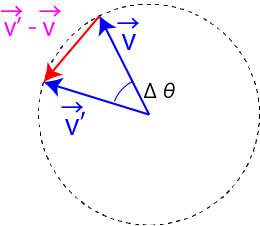
ここで,角速度の大きさは変わらないので,
\( \Large \displaystyle \vert \vec{v'} \vert =\vert \vec{v} \vert = v \)
となります.また,加速度は,
\( \Large \displaystyle \vec{ \alpha} =\frac{ \vec{v'} - \vec{v}}{ \Delta t} \)
となりますが,最初の弧度法から,
\( \Large \displaystyle \vert \vec{v'} - \vec{v} \vert \simeq v \cdot \Delta \theta \)
となりますので,
\( \Large \displaystyle \alpha = \frac{\vert \vec{v'} - \vec{v} \vert}{ \Delta t} \simeq v \cdot \frac{\Delta \theta}{ \Delta t} = v \cdot \omega \)
となります.先に述べた速さの関係式を考慮すると,
\( \Large \displaystyle \alpha = v \cdot \omega = r \cdot \omega^2 \)
となり,働く力,遠心力,は,
\( \Large \displaystyle F = m \cdot \alpha = m \cdot r \cdot \omega^2 \)
となります.
次に,
加速度ベクトルは速度ベクトルに直交する
を検討していきましょう.