地震のマグニチュードとは?
先日(2025.07.30),カムチャツカ半島で大きな地震があり,津波警報が日本,ハワイなどにおいて1日中出されました.
阪神淡路大震災(1995),東日本大震災(2011),大阪北部地震(2018)
を経験した私にとっても,気になる事象です.最近大阪で目立った地震がないことも気になります.
そこで,よく提供される情報の一つに,マグニチュード,という値があります.
よく,マグニチュードが1上がると,地震のエネルギーは,32倍上がる,
と言われていますが,
どのような計算式?
1上がると,となると比較するマグニチュードには関係ない?
32倍,というと2の5乗,に関係する?
など,よく知らないことが多いです.
ネットなどで調べると,たくさんの情報があり,結構複雑で,いろいろな計算式があるようです.
気象庁のHP,に日本で使用されるマグニチュードの解説がありますが,どうも,
経験則に基づいた計算式
のようなので,ここでは,
歴史,計算式の導出過程
などには手を触れず,単純に計算式,のみを考えていきます.
・計算式
地震波の形で放出されるエネルギーの大きさをE(J),マグニチュードをMとすると,
\( \Large \displaystyle log_{10} E = 4.8 + 1.5 M \)
の関係があるとのことです.ほかにもいろいろな計算式があるようですが,基本的な式の形態は同じです.対数がかかっていることに注意です.
書き換えると,
\( \Large \displaystyle 1.5 \ M = log_{10} E - 4.8 \)
\( \Large \displaystyle = log_{10} E -log_{10} (10^{4.8}) \)
\( \Large \displaystyle = log_{10} \frac{E}{10^{4.8}} \)
\( \Large \displaystyle 1.5 M = log_{10} \frac{E}{10^{4.8}} \)
となります.ここで,二つのマグニチュード,M,Ma=M+a,を考えます.
\( \Large \displaystyle 1.5(M+a) = log_{10} \frac{E_a}{10^{4.8}} \)
\( \Large \displaystyle 1.5M+1.5a = log_{10} \frac{E_a}{10^{4.8}} \)
\( \Large \displaystyle log_{10} \frac{E}{10^{4.8}}+1.5a = log_{10} \frac{E_a}{10^{4.8}}\)
\( \Large \displaystyle 1.5a = log_{10} \frac{E_a}{10^{4.8}} - log_{10} \frac{E}{10^{4.8}}\)
\( \Large \displaystyle 1.5a = log_{10}\frac{ \frac{E_a}{10^{4.8}}}{ \frac{E}{10^{4.8}}}\)
\( \Large \displaystyle 1.5a = log_{10}\frac{ E_a}{E}\)
\( \Large \displaystyle \frac{ E_a}{E} = 10^{1.5a}\)
となります. 10のべき乗,で効いてくることがわかります.
マグニチュードが,1,変わると,
\( \Large \displaystyle \frac{ E_a}{E} = 10^{1.5 \times 1} \simeq \color{red}{31.62} \)
マグニチュードが,2,変わると,
\( \Large \displaystyle \frac{ E_a}{E} = 10^{1.5 \times 2} = \color{red}{1000} \)
マグニチュードが,0.1,変わると,
\( \Large \displaystyle \frac{ E_a}{E} = 10^{1.5 \times 0.1} \simeq \color{red}{1.413} \)
倍,変化することになります.下のマグニチュードとは関係ないことがわかります.
0.1刻みでその変化を見ると,
| ΔMagnitude | エネルギーは何倍? |
| 0.1 | 1.41 |
| 0.2 | 2.00 |
| 0.3 | 2.82 |
| 0.4 | 3.98 |
| 0.5 | 5.62 |
| 0.6 | 7.94 |
| 0.7 | 11.22 |
| 0.8 | 15.85 |
| 0.9 | 22.39 |
| 1.0 | 31.62 |
となります.マグニチュードの値が上がるとべき乗則なので,飛躍的にエネルギーが上がる,ということは,想定内の地震のエネルギーにおいては(地球が壊滅するぐらいのエネルギーは考えない)マグニチュードの値がサチる,ということになりますね.
つまり,現状ではマグニチュードの値が8とか9であるが,それ以上(10とか)は起こる確率がほぼ皆無,ということでしょう.
これを「マグニチュードの飽和」と呼ぶ,らしいです.
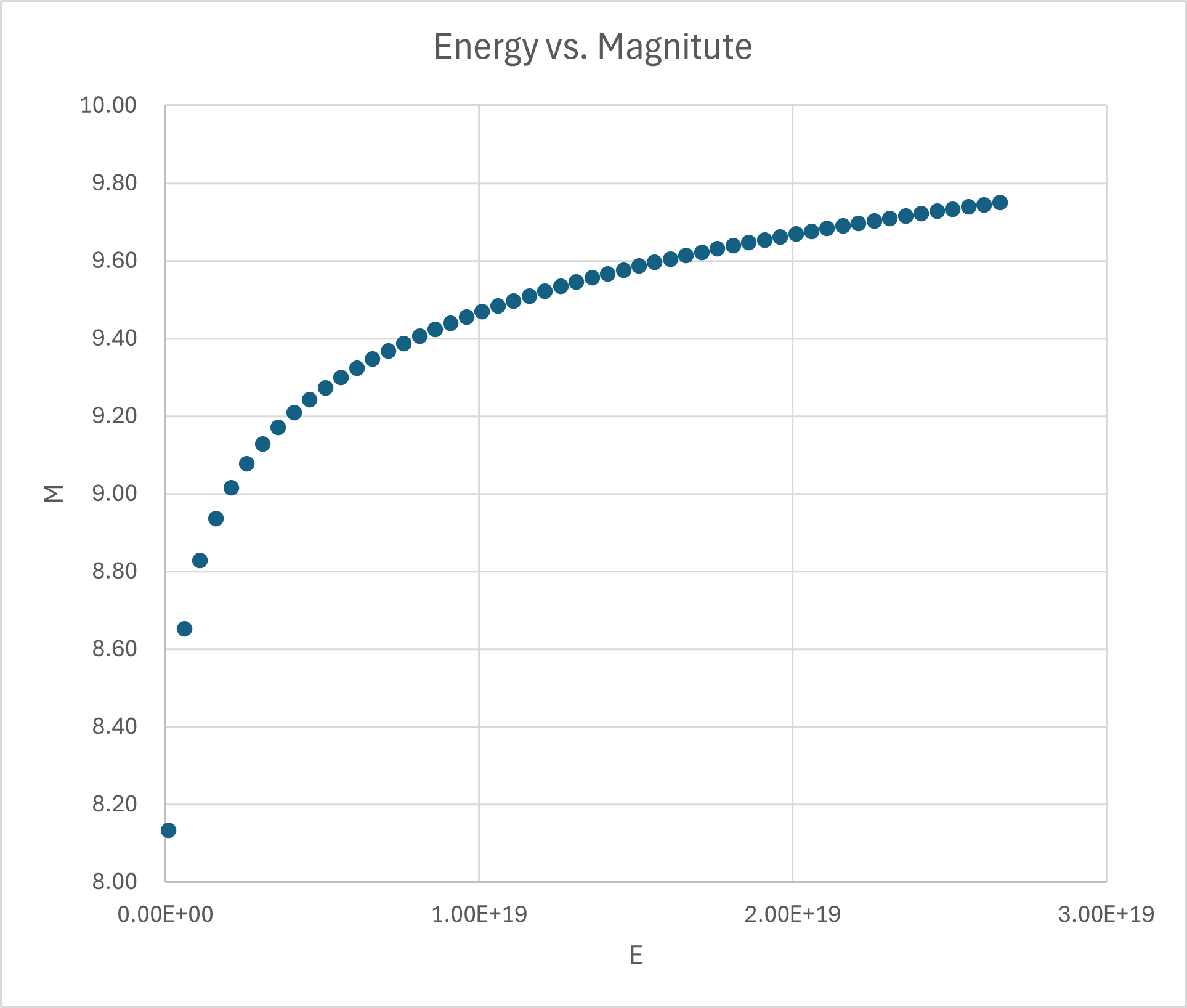
グラフ化すると,

となり,地震のエネルギー(横軸)が大きくなっても,マグニチュード(縦軸)にはそれほど変化がないことになりますね.
今後,東日本大震災を上回る大地震が起きても,マグニチュードで換算すると大したことがない,というようなイメージになっちゃいそうですね.
そこで,飽和しないための新たな指針,モーメント・マグニチュード,というものもあるらしいです..
ただ,気象庁のサイトを見ると,一般的なマグニチュードを利用しているようです.これらの換算式は....よくわかりません.
ちなみに,上記の地震のマグニチュードを調べると,
| 地震名 | 日付 | マグニチュード | 東日本大震災に比べて |
| 阪神淡路大震災 | 1995 | 7.3 | 0.02 |
| 東日本大震災 | 2011 | 9.0 | 1 |
| 大阪北部地震 | 2018 | 6.1 | 0.001 |
| カムチャツカ | 2025 | 8.7-8.8 | 0.50-0.63 |
となります.東日本大震災に比べて,にはなんの意味もありませんが,東日本大震災の破壊的なエネルギーの大きさが理解できます.
マグニチュードと震源からの距離,が我々は気をつける必要がありますね.
・備考
よく,マグニチュードが1変わるとエネルギーは32倍変わる,と報道されているので,32=25と関連するのでは,思っていました. しかし,
\( \Large \displaystyle \frac{ E_a}{E} = 10^{1.5 \times 1} \simeq 31.62 \)
なので,確認してみましょう.
\( \Large \displaystyle 2^x= 10^{1.5 \times 1} \)
\( \Large \displaystyle log_{10} \ 2^x= log_{10} \ 10^{1.5 \times 1} \)
\( \Large \displaystyle x \ log_{10} \ 2= 1.5 \)
\( \Large \displaystyle x = \frac{1.5}{ log_{10} } \simeq 4.983 \)
となり,2のべき乗とは関係ないことがわかります.
兎にも角にも,日本に住んでいる限り地震と付き合っていかなければならないので,防災,減災,さらには地震予測の地道な基礎研究が必要となりますね.
我々はついつい,何%の確率?,などと盲目的に信じたり非難したりしますが,どんな原理で予測しているのかも理解していきたいです.
防災,のためには,防災ブック「東京くらし防災」・「東京防災」,が便利です(前のバージョンのほうが読みやすかったかな?).
東京,と書いてありますが,日本全国,世界中で役立つブックです.