ラプラス変換_運動方程式 - k>ω

・ k > ω

平方根の中の値が実数になるので，そのまま計算して，

\( \Large \displaystyle A \equiv -(- k - \sqrt{k^2 - \omega^2}) = k + \sqrt{k^2 - \omega^2}\)

\( \Large \displaystyle B \equiv -(-k + \sqrt{k^2 - \omega^2}) = k - \sqrt{k^2 - \omega^2}\)

とすると，

\( \Large \displaystyle F(s) =\frac{ s \ f(0) + f'(0) + 2k \ f(0)}{( s+A)(s +B) } \)

右辺を部分分数分解を行うと，

\( \Large \displaystyle F(s) =\left\{ s \ f(0) + f'(0) + 2k \ f(0) \right\}\frac{ 1}{( s+A)(s +B) } \)

\( \Large \displaystyle \hspace{30 pt} =
\frac{ \alpha}{ s+A}
+ \frac{\beta}{s+B } \)

\( \Large \displaystyle
\frac{ \alpha}{ s+A} + \frac{\beta}{s+B }
= \frac{ \alpha( s+B) + \beta ( s+A) }{( s+A)(s +B) } \)

分子を整理すると，

\( \Large \displaystyle \alpha( s+B) + \beta ( s+A)
= ( \alpha + \beta)s + \alpha \ B + \beta \ A\)

sの項では

\( \Large \displaystyle \alpha + \beta= f(0) \)

ｓ以外の項では，

\( \Large \displaystyle \alpha \ B + \beta \ A
= \alpha \left\{ k - \sqrt{k^2 - \omega^2} \right\}+ \beta \left\{ k + \sqrt{k^2 - \omega^2} \right\} \)

\( \Large \displaystyle = ( \alpha + \beta) k - (\alpha - \beta) \sqrt{k^2 - \omega^2}
=f'(0) + 2k \ f(0) \)

\( \Large \displaystyle k \ f(0) - (\alpha - \beta) \sqrt{k^2 - \omega^2}
=f'(0) + 2k \ f(0) \)

\( \Large \displaystyle (\alpha - \beta) \sqrt{k^2 - \omega^2}
= - k \ f(0) -f'(0) - 2k \ f(0) \)

\( \Large \displaystyle \alpha - \beta
=-\frac{ f'(0) + k \ f(0)}{\sqrt{k^2 - \omega^2}} \)

\( \Large \displaystyle \alpha + \beta= f(0) \)

との関係から，

\( \Large \displaystyle \alpha = \frac{1}{2} \left[ f(0)-\frac{ f'(0) + k \ f(0)}{\sqrt{k^2 - \omega^2}} \right]\)

\( \Large \displaystyle = \frac{ f(0) \sqrt{k^2 - \omega^2} - f'(0) - k \ f(0)}{2 \sqrt{k^2 - \omega^2}} \)

\( \Large \displaystyle = -\frac{ f'(0) +( k - \sqrt{k^2 - \omega^2} ) \ f(0)}{2 \sqrt{k^2 - \omega^2}} \)

\( \Large \displaystyle \beta= f(0) - \alpha
= f(0) - \left[ -\frac{ f'(0) +( k - \sqrt{k^2 - \omega^2} ) \ f(0)}{2 \sqrt{k^2 - \omega^2}} \right] \)

\( \Large \displaystyle =\frac{2 f(0) \sqrt{k^2 - \omega^2} + f'(0) +( k - \sqrt{k^2 - \omega^2} ) \ f(0)}{2 \sqrt{k^2 - \omega^2}} \)

\( \Large \displaystyle =\frac{ f'(0) +( k + \sqrt{k^2 - \omega^2} ) \ f(0)}{2 \sqrt{k^2 - \omega^2}} \)

したがって，逆ラプラス変換を行うと，

\( \Large \displaystyle F(s) =\frac{ \alpha}{ s+A} + \frac{\beta}{s+B } \)

\( \Large \displaystyle x(t) = \alpha \ e^{-At} + \beta \ e^{-Bt} \)

ここで，

\( \Large \displaystyle \alpha = -\frac{ f'(0) +( k - \sqrt{k^2 - \omega^2} ) \ f(0)}{2 \sqrt{k^2 - \omega^2}} \)

\( \Large \displaystyle \beta =\frac{ f'(0) +( k + \sqrt{k^2 - \omega^2} ) \ f(0)}{2 \sqrt{k^2 - \omega^2}} \)

\( \Large \displaystyle A = k + \sqrt{k^2 - \omega^2}\)

\( \Large \displaystyle B = k - \sqrt{k^2 - \omega^2}\)

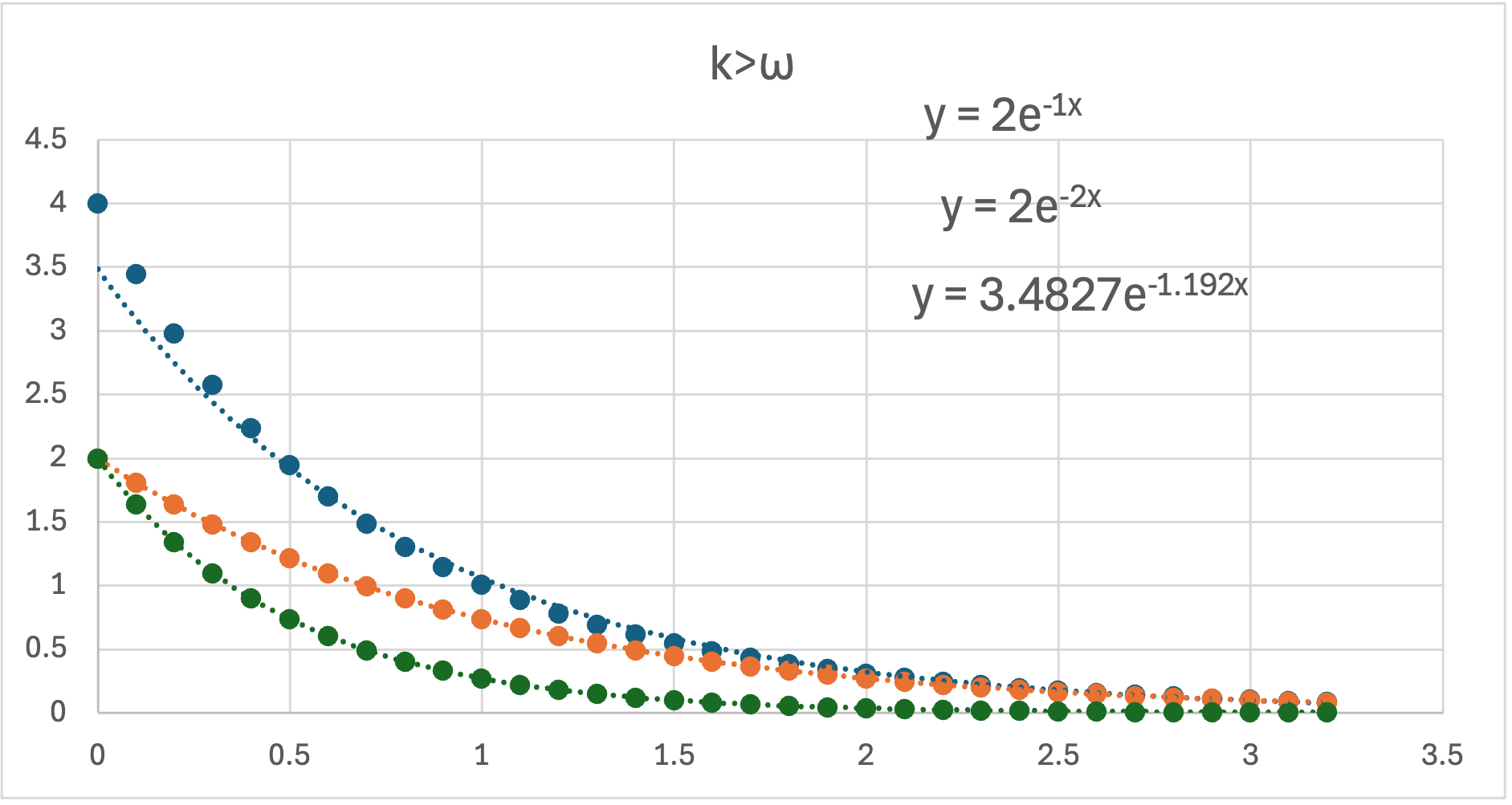
となります．つまり，2つの指数関数の和となります．

単純な指数関数ではフィットできない曲線になるようです．

これを，超過減衰，と呼ぶようです．

x(0), x'(0)，を色々変えてみると，

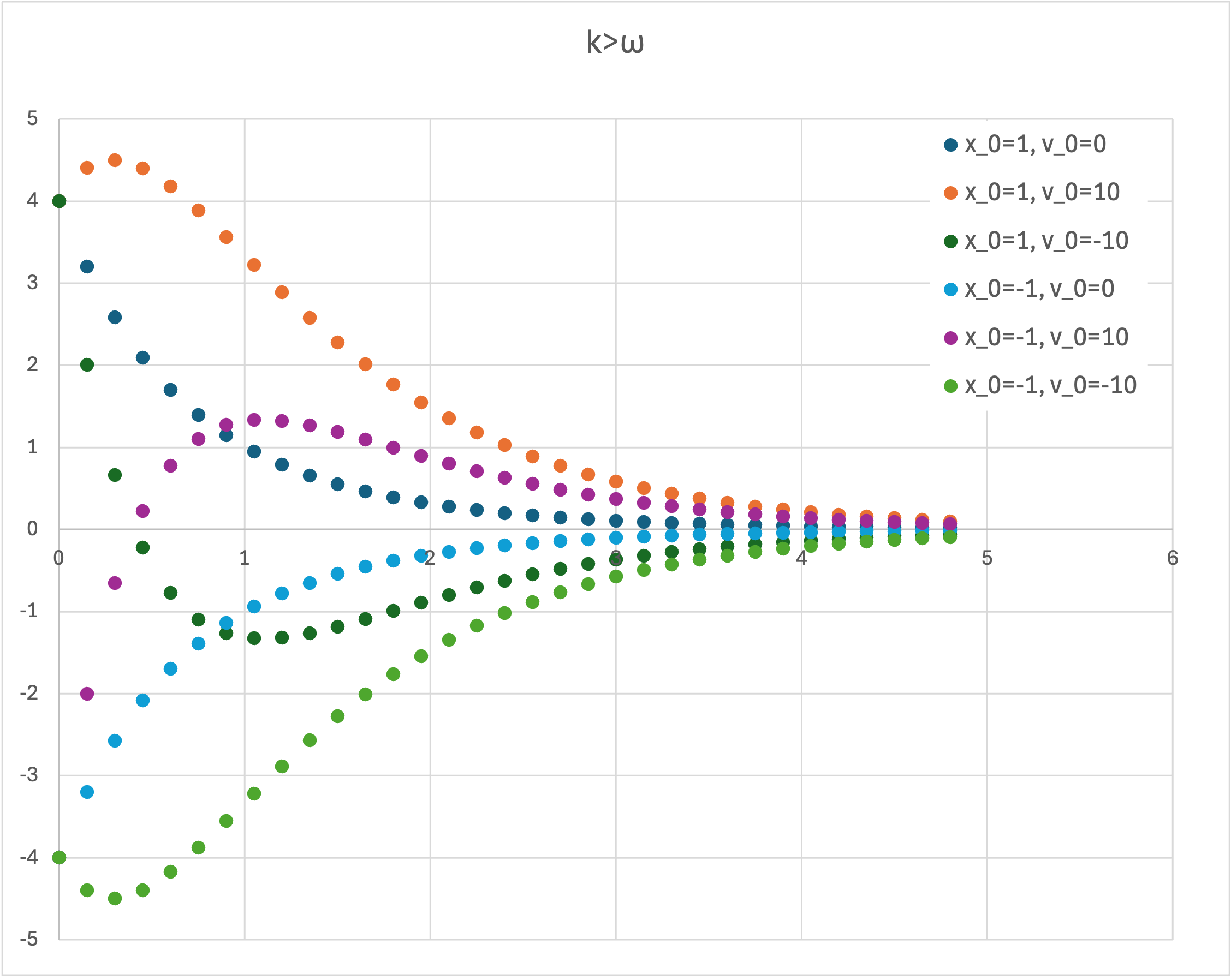
このように，オーバーシュートする場合があることがわかります．

次は， k=ω，の場合です．