フーリエ級数展開-08

次は三角波

・三角波

三角波，

\( \Large \displaystyle f(x) = |x| \hspace{20pt} ( - \pi \leq x < \pi) \)

書き換えると，

\( \Large = \left\{ \begin{array}{c} \hspace{10pt} -x \hspace{20pt} ( \pi \leq x < 0) \\ \hspace{20pt} x \hspace{20pt} (0 \leq x < \pi) \end{array} \right. \)

の場合を考えます．

フーリエ級数展開は，周期が　‐π～π，の場合には，

\( \Large \displaystyle f(x) = \color{red}{\frac{a_0}{2}} + \sum_{n=1}^{ \infty} \left( a_n \ cos \ (n x) + b_n \ sin \ (n x) \right) \)

\( \Large \displaystyle a_0 = \color{red}{\frac{1}{\pi}} \int_{- \pi}^{ \pi} f(x) \ dx \)

\( \Large \displaystyle a_n = \frac{1}{\pi} \int_{ - \pi}^{ \pi} f(x) \ cos \ \left( nx \right) \ dx \)

\( \Large \displaystyle b_n = \frac{1}{\pi} \int_{ - \pi}^{ \pi} f(x) \ sin \ \left( nx \right) \ dx \)

は，ここ，で解説しました．

・a₀

積分範囲によって，f(x)の値が異なるので，それぞれの領域の積分に分けていきます．

\( \Large \displaystyle \frac{a_0}{2} = \frac{1}{2} \color{red}{\frac{1}{\pi}}\int_{- \pi}^{ \pi} f(x) \ dx
= \frac{1}{2 \pi} \left\{ \int_{- \pi}^{ 0} (-x) \ dx + \int_{0}^{ \pi} (x) \ dx \right\}
= \frac{1}{2 \pi} \left\{ \left[ - \frac{1}{2} x^2 \right]_{- \pi}^0 + \left[ \frac{1}{2} x^2 \right]_0^{ \pi}\right\}
= \frac{1}{2 \pi} \left\{ \frac{1}{2} \pi^2 + \frac{1}{2} \pi^2 \right\} = \color{red}{\frac{1}{2} \pi }
\)

・a_n

\( \Large \displaystyle a_n = \frac{1}{\pi} \int_{ - \pi}^{ \pi} f(x) \ cos \ \left( nx \right) \ dx \)

ですが，f(x)，cos (nx)，ともに偶関数となります．したがって，積分範囲を半分（0～π）で計算して2倍すればいいことになりますので，

\( \Large \displaystyle a_n = \frac{2}{\pi} \int_{ 0}^{ \pi} f(x) \ cos \ \left( nx \right) \ dx = \frac{2}{\pi} \int_{ 0}^{ \pi} x \ cos \ \left( nx \right) \ dx \)

を計算すればいいことになります．

これは，ここ，で説明した，瞬間部分積分，を使えば簡単に解け，

\( \Large \displaystyle \int x \ cos \ (n x) \ dx \)

を考えていきます．瞬間部分積分を使えば，

\( \Large \displaystyle \int x \ cos \ (n x) \ dx =\frac{1}{n} x \ sin \ ( n x) + \frac{1}{n^2} x \ cos \ (nx) + C\)

となります．したがって，

\( \Large \displaystyle a_n = \frac{2}{\pi} \int_{ 0}^{ \pi} x \ cos \ \left( nx \right) \ dx \)

\( \Large \displaystyle = \frac{2}{\pi} \left[ \frac{1}{n} x \ sin \ ( n x) + \frac{1}{n^2} x \ cos \ (nx) \right]_0^{ \pi} \)

\( \Large \displaystyle = \frac{2}{\pi} \left[ \frac{1}{n} \{ \pi \ sin \ ( n \pi) - 0 \ sin \ (n \ 0) \} + \frac{1}{n^2} \{ cos \ (n \pi) - 1 \} \right] \)

\( \Large \displaystyle = \frac{2}{\pi n^2 } \{ cos \ (n \pi) - 1 \} \)

\( \Large \displaystyle = \frac{2}{\pi n^2 } \{ (-1)^n - 1 \} \)

\( \Large = \left\{ \begin{array}{c} \hspace{10pt} 0 \hspace{20pt} ( n \ is \ even ) \\ \hspace{20pt} - \frac{4}{ \pi n^2} \hspace{20pt} ( n \ is \ odd) \end{array} \right. \)

となります．

・b_n

\( \Large \displaystyle b_n = \frac{1}{\pi} \int_{ - \pi}^{ \pi} f(x) \ sin \ \left( nx \right) \ dx \)

ですが，f(x)が偶関数，sinが奇関数なので，奇関数となります． -π～πの積分なので奇関数の場合は０となります，したがって，

\( \Large \displaystyle b_n =0 \)

となります．

したがって，まとめると，

\( \Large \displaystyle f(x) = \frac{1}{2} \pi + \sum_{n=1}^{\infty} \frac{2}{\pi n^2 } \{ (-1)^n - 1 \} \cdot cos (nx) \)

\( \Large \displaystyle f(x) = \frac{1}{2} \pi - \frac{4}{ \pi} \left\{ cos x + \frac{1}{3^2} cos (3x) + + \frac{1}{5^2} cos (5x) +...... \right\} \)

となります．

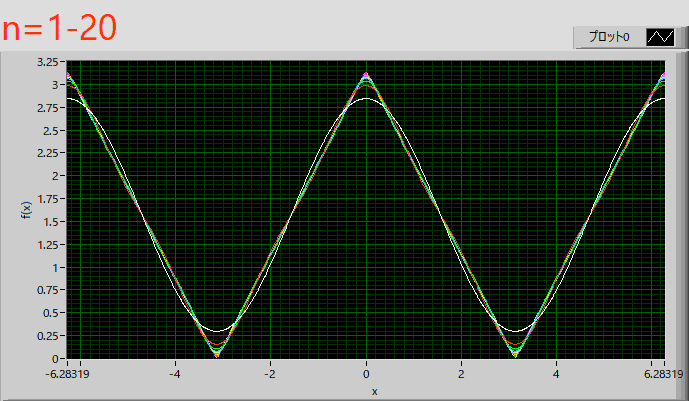
グラフで図示すると，

となります．三角はと正弦波は似ているので，すぐに収束しているみたいですね．

次は，ノコギリ波，です．