F検定-02

F分布の式を見てみると，

\(\Large \displaystyle f_X (x) = \frac{\Gamma \left( \frac{n_1 + n_2 }{2} \right)}{ \Gamma \left( \frac{n_1 }{2} \right) \Gamma \left( \frac{ n_2 }{2} \right)}
n_1^{ \frac{n_1}{2}} n_2^{ \frac{n_2}{2}}
\left( \frac{1}{ n_1 x + n_2} \right)^{ \frac{n_1 + n_2}{2}}
x^{ \frac{n_1}{2} -1} \)

実は，各分散の値自体は関係なく，データ数のみの関数となっていることがわかります．

実際に，n₁=10, n₂=8とすると，

となることがわかります．

データ数を倍にして，n₁=20, n₂=16とすると，

となり，分布が狭まることがわかります．

つぎに，シミュレーション．ある分散値を設定して，正規分布を発生させます．その分布から上記の数だけ取り出して不偏分散を算出し，これを2セット用意します．その比の分布のヒストグラムにして表すと，

n₁=10, n₂=8

n₁=20, n₂=16

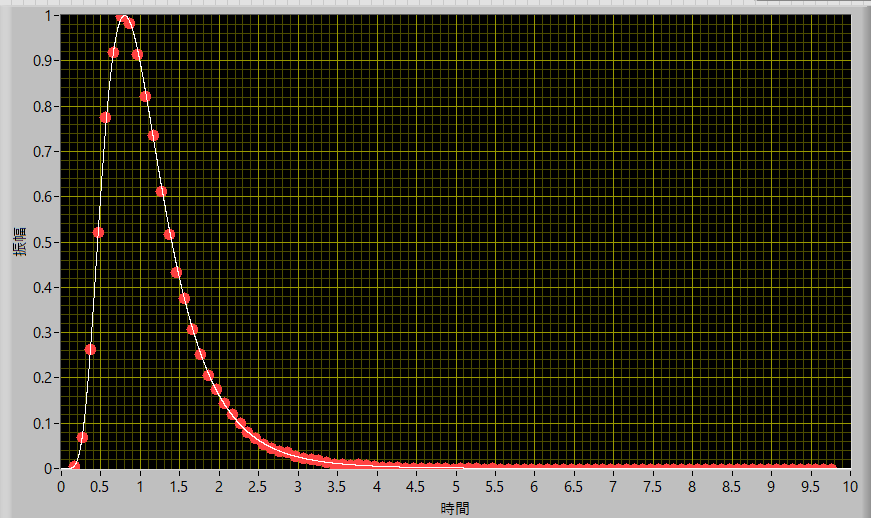
とよく合うことがわかります．

つぎに，実際に具体的なデータを用意してF検定をしてみましょう．