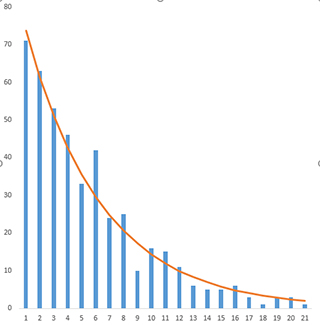
サイコロを振って，”６”が出るまでの回数はどのような分布になるか?

さて，一分子計測による解析手法，というコーナーになぜ，さいころ?と疑問に思われる方もおられるかと思いますが，結構重要な問題です．

サイコロを振って，”６”，が出る確率は?という問いはすぐにわかりますね，答えは，１／６，です．
では，サイコロを振って，”６”が出るまで何回サイコロを振るか?その分布は?というのが，今回の問題です．

まずは，一回で６が出る確率は，１／６，です．
では，２回目で６が出る確率は，１／６，ではありません．
この問いをもっと正確に記述すると，
　１回目は６が出なくて，２回目に６が出る確率
なのです．
ですので，その確率は，

\( \Large \displaystyle \left( 1 - \frac{1}{6} \right) \times \frac{1}{6}\)
となるのです．

つまり，
　１回目　：　\( \Large \hspace{ 108pt} \displaystyle \frac{1}{6} \)
　２回目　：　\( \Large \hspace{ 12pt} \displaystyle \left( 1 - \frac{1}{6} \right) \hspace{ 18pt} \times \frac{1}{6}\)
　３回目　：　　\( \Large \displaystyle \left( 1 - \frac{1}{6} \right)^2 \hspace{ 14pt} \times \frac{1}{6}\)
　ｎ回目　：　　\( \Large \displaystyle \left( 1 - \frac{1}{6} \right)^{n-1} \times \frac{1}{6}\)

という法則性があります．確率で表すと，

　\( \Large \displaystyle P(n) = \left( 1 - \frac{1}{6} \right)^{n-1} \times \frac{1}{6}\)

となります．このままでは使いづらいので，指数に直すと，

　\( \Large \displaystyle ln \ P(n) = ln \left[ \left( \frac{5}{6} \right)^{n-1} \times \frac{1}{6} \right] \)

　\( \Large \displaystyle \hspace{ 49pt} = (n-1) \cdot ln \left( \frac{5}{6} \right) + ln \frac{1}{6} \)

　\( \Large \displaystyle \hspace{ 49pt} = n \cdot ln \left( \frac{5}{6} \right) - ln \left( \frac{5}{6} \right)+ ln \frac{1}{6} \)

　\( \Large \displaystyle \hspace{ 49pt} = n \cdot ln \left( \frac{5}{6} \right) + ln \frac{1}{5} \)

　\( \Large \displaystyle P(n) = \frac{1}{5} \ EXP \left[ n \cdot ln \left( \frac{5}{6} \right) \right] \)

となります．ln(5/6)はマイナスの値なので，単調減少する指数関数となります．

このことが何を意味するかというと，
　ランダムな現象でも，そのイベントが起こるまでの回数，時間の分布は指数関数となる
と言うことです．

つまり，さいころを振って６が出る回数は１／６ですが，６が出るまでの回数は６回以下で起こる確率がとても多い．
と言うことです．
その代わり，何回サイコロをふっても，６が出ない場合（１００回ふっても，１０００回ふっても）もあり得ます．

上のグラフは，４４２回のトライアルでの結果です（エクセルで計算しました）．
計算通り，指数関数となっていることがわかりますね．

あまりよい例ではないですが，飛行機事故，は一度起こると連鎖して次の事故も起こるように感じます．
しかし，もし飛行機事故がお互いに関連なく，ランダムに発生するとしても，事故と事故との間隔は上記のように，指数関数となるので短い確率の方が高くなります．
なので，あたかも連鎖しているように感じ取れるのです（もちろん，気象や人的要因で連鎖する可能性もあります）．
このあたりは，このサイト，に詳しく書かれています．

また，この議論は化学反応においても適用できます．
単純な一次反応を考えてみると，

\( \Large \ce{A ->[\ k \ ] B} \)

という反応を考えます．
これは，Aと言う状態からBと言う状態へ速度定数，ｋ，（単位は１/s）で遷移する，というものです．
もし，ｋ＝１００，とすると，１秒間に１００回，となりますので，１回にかかる時間は１０msとなります．
しかし，１０msごとに遷移が起こる，というわけではなく，平均１０ms，であることに注意してください．
この遷移がランダムに起こる，と考えると，上記の計算が適用できます．
つまり，
　ある分子Aは１０msよりも早くBに遷移する
　ある分子Aは１０msよりも遅くBに遷移する
　１０msよりも早く遷移する割合の方が多い
　しかし，平均は１０msである
と言うことになるのです．
詳しくは，一次反応に対する持続時間の分布について，をご覧ください．

次に，上の確率密度がきちんと規格化されているか，平均値はいくらか，を調べてみましょう．