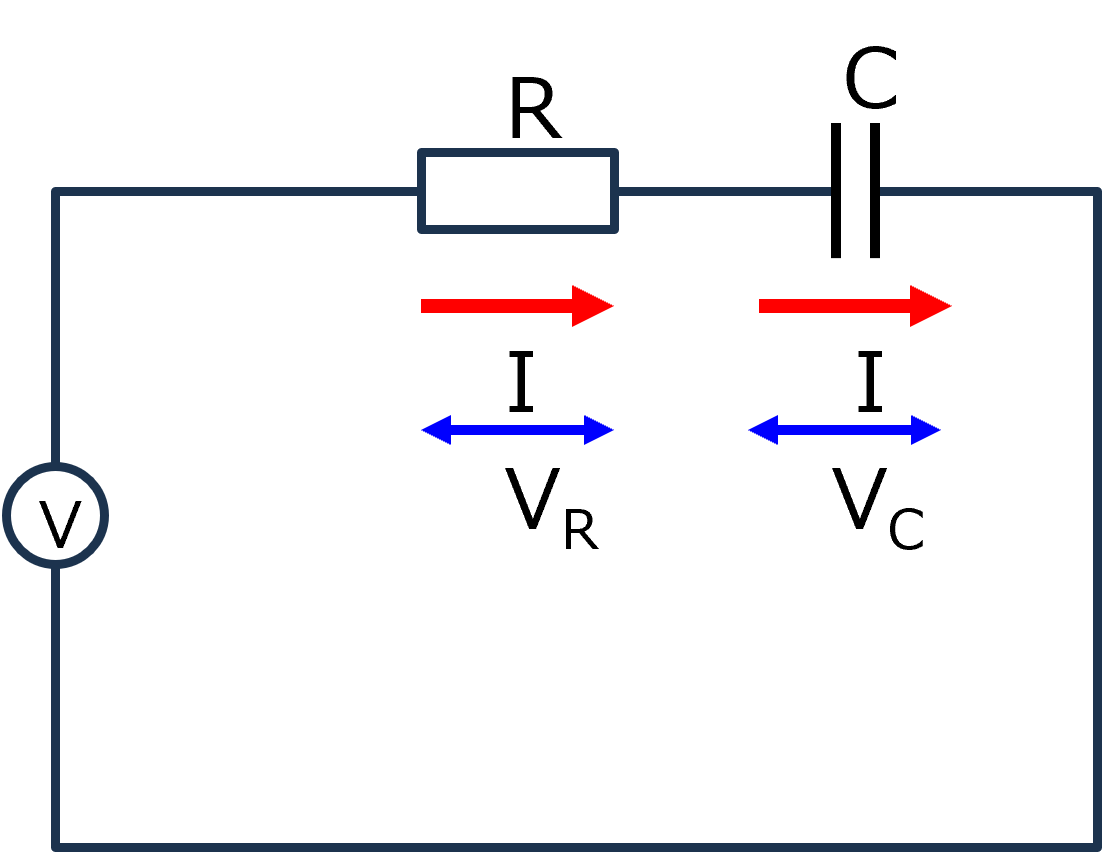
回路-09-5
RC直列交流回路をラプラス変換で真面目に解く - 電圧を主体に考える

RとCが直列に並んだ交流回路をラプラス変換で電圧を主体にまじめに考えます.式は,
\(\Large \displaystyle \frac{d}{dt} V_C (t) =- \frac{1}{RC} V_C (t) + \frac{1}{RC}V_0 \cdot e^{j \omega t} \)
でした.変形して,
\(\Large \displaystyle \frac{d}{dt} V_C (t) + a \ V_C (t) = a \ V_0 \cdot e^{j \omega t} \)
\(\Large \displaystyle \left(a \equiv \frac{1}{RC}\right) \)
ラプラス変換をおこなうと,
\(\Large \displaystyle sF(s)-V_C(0)\ + a \ F(s) =a\ V_0 \ \frac{1}{s - j \omega} \)
\(\Large \displaystyle (s+a)F(s) = a\ V_0 \ \frac{1}{s - j \omega} + V_C(0) \)
\(\Large \displaystyle F(s) = a\ V_0 \ \frac{1}{(s - j \omega)(s+a)} + \frac{V_C(0)}{s+a} \)
となるので,右辺第一項を,
\(\Large \displaystyle \frac{1}{(s - j \omega)(s+a)} = \frac{A}{s - j \omega} + \frac{B}{s+a} \)
\(\Large \displaystyle = \frac{A(s+a)+B(s - j \omega)}{(s - j \omega)(s+a)} \)
\(\Large \displaystyle = \frac{s(A+B)+aA - j \omega B}{(s - j \omega)(s+a)} \)
\(\Large \displaystyle A+B=0 \rightarrow B = -A \)
\(\Large \displaystyle aA - j \omega B = aA + j \omega A = (a + j \omega) A = 1 \)
\(\Large \displaystyle A=\frac{1}{a + j \omega} \)
\(\Large \displaystyle B = - \frac{1}{a + j \omega} \)
となります.したがって,
\(\Large \displaystyle F(s) = a\ V_0 \ \frac{1}{a + j \omega}( \frac{1}{s - j \omega} - \frac{1}{s+a}) + \frac{V_0}{s+a} \)
\(\Large \displaystyle = V_0 \ \frac{a}{a + j \omega}( \frac{1}{s - j \omega} - \frac{1}{s+a}) + \frac{V_0}{s+a} \)
\(\Large \displaystyle = V_0 \ \frac{1/RC}{1/RC + j \omega}( \frac{1}{s - j \omega} - \frac{1}{s+a}) + \frac{V_0}{s+a} \)
\(\Large \displaystyle = V_0 \ \frac{1}{1 + j \omega RC}( \frac{1}{s - j \omega} - \frac{1}{s+a}) + \frac{V_0}{s+a} \)
となります.逆ラプラス変換を行って,
\(\Large \displaystyle V_C (t) = V_0 \ \frac{1}{1 + j \omega RC}( e^{ j \omega t} - e^{-\frac{1}{RC} t}) + V_0 \ e^{-\frac{1}{RC} t} \)
\(\Large \displaystyle I(t) = C \cdot \frac{d}{dt} V_C (t) \)
\(\Large \displaystyle =V_0 \ \frac{1}{1 + j \omega RC}( j \omega \ e^{ j \omega t} + \frac{1}{RC}e^{-\frac{1}{RC} t}) \)
\(\Large \displaystyle =V_0 \cdot \frac{C}{1 + j \omega RC} \left( j \omega \ e^{j \omega t} + \frac{1}{RC} e^{ - \frac{1}{RC} t}\right) - V_0 \frac{1}{RC} e^{ - \frac{1}{R} t}) \)
\(\Large \displaystyle =V_0 \cdot \frac{j \omega C}{1 + j \omega RC} e^{j \omega t} + \frac{1}{1 + j \omega RC}\frac{1}{R} e^{ - \frac{1}{RC} t} - V_0 \frac{1}{R} e^{ - \frac{1}{RC} t}) \)
\(\Large \displaystyle =V_0 \cdot \frac{j \omega C}{1 + j \omega RC} e^{j \omega t} + V_0 \frac{1 - 1 - j \omega RC}{1 + j \omega RC}\frac{1}{R} e^{ - \frac{1}{RC} t} ) \)
\(\Large \displaystyle =V_0 \cdot \frac{j \omega C}{1 + j \omega RC} e^{j \omega t} + V_0\frac{ - j \omega C}{1 + j \omega RC} e^{ - \frac{1}{RC} t} ) \)
\(\Large \displaystyle =V_0 \cdot \frac{j \omega C}{1 + j \omega RC} \left( e^{j \omega t} - e^{ - \frac{1}{RC} t} \right) \)
\(\Large \displaystyle I(t) = V_0 \cdot \frac{j \omega}{R (a+j \omega)} \left( e^{ j \omega t} - e^{-at} \right) \)
\(\Large \displaystyle = V_0 \cdot \frac{j \omega}{\frac{1}{C}+j \omega R } \left( e^{ j \omega t} - e^{- \frac{1}{RC}t} \right) \)
\(\Large \displaystyle = V_0 \cdot \frac{j \omega C}{1+j \omega RC } \left( e^{ j \omega t} - e^{- \frac{1}{RC}t} \right) \)
\(\Large \displaystyle = V_0 \cdot \frac{j \omega C + \omega^2 R C^2}{1+ (\omega RC)^2 } \left( e^{ j \omega t} - e^{- \frac{1}{RC}t} \right) \)
\(\Large \displaystyle = V_0 \cdot \frac{ \frac{j}{\omega C} + R }{\frac{1}{ (\omega C)^2}+ R^2 } \left( e^{ j \omega t} - e^{- \frac{1}{RC}t} \right) \)
となり,一致します.
後の展開は同じですが,きちんと書くと,
\(\Large \displaystyle = V_0 \cdot \frac{R + \frac{j}{ \omega C}}{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}} \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot \left( e^{ j \omega t} - e^{- \frac{1}{ RC} t} \right) \)
ここで,複素数の項を指数に置き換える.
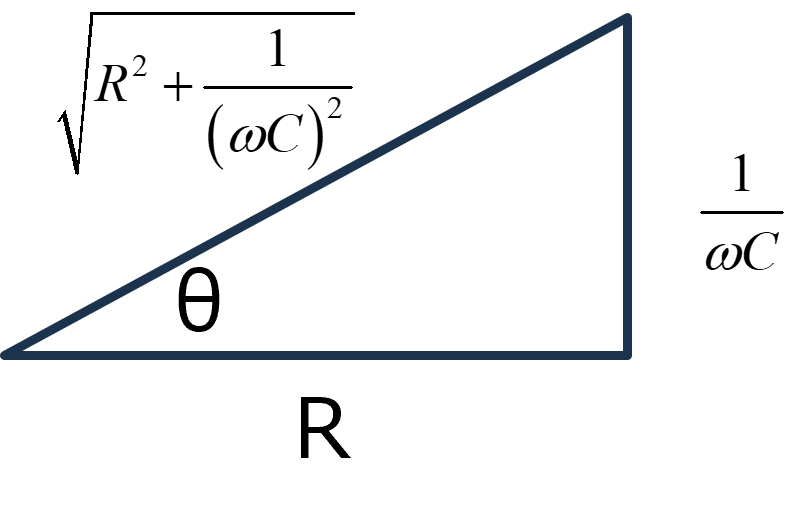
\(\Large \displaystyle cos \ \theta = \frac{R }{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}\)
\(\Large \displaystyle j \cdot sin \ \theta = \frac{ \frac{j}{ \omega C}}{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}\)
\(\Large \displaystyle e^{ j \ \theta} =cos \ \theta + j \cdot sin \ \theta \)
より,
\(\Large \displaystyle \frac{R + \frac{j}{ \omega C}}{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}} = e^{ j \ \theta} \)
ここで,
\(\Large \displaystyle tan \ \theta = \frac{1} {\omega RC} \)
となります.したがって,
\(\Large \displaystyle I(t) = V_0 \cdot \frac{R + \frac{j}{ \omega C}}{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}} \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot \left( e^{ j \omega t} - e^{- \frac{1}{ RC} t} \right) \)
\(\Large \displaystyle = V_0 \cdot e^{ j \ \theta} \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot \left( e^{ j \omega t} - e^{- \frac{1}{ RC} t} \right)\)
\(\Large \displaystyle = V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot \left\{ e^{ j (\omega t + \theta)} - e^{ j \ \theta} \cdot e^{- \frac{1}{ RC} t} \right\}\)
となります.ここで,三角関数に戻すために,虚数部分のみ取り出すと,
\(\Large \displaystyle Im [ I(t) ] = Im \left[V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot e^{ j (\omega t + \theta)} \right]
- Im \left[V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot e^{ j \ \theta} \cdot e^{- \frac{1}{ RC} t} \right] \)
\(\Large \displaystyle = V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot sin (\omega t + \theta)
- V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot sin \ \theta \cdot e^{- \frac{1}{ RC} t} \)
十分な時間が経てば,第二項は0となるので,
\(\Large \displaystyle I(t) \sim \frac{V_0 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot sin (\omega t + \theta) \)
\(\Large \displaystyle \theta = tan^{-1} \ \frac{1} {\omega RC} \)
となり,インピーダンスを用いた結果と一致します.