回路-09-3

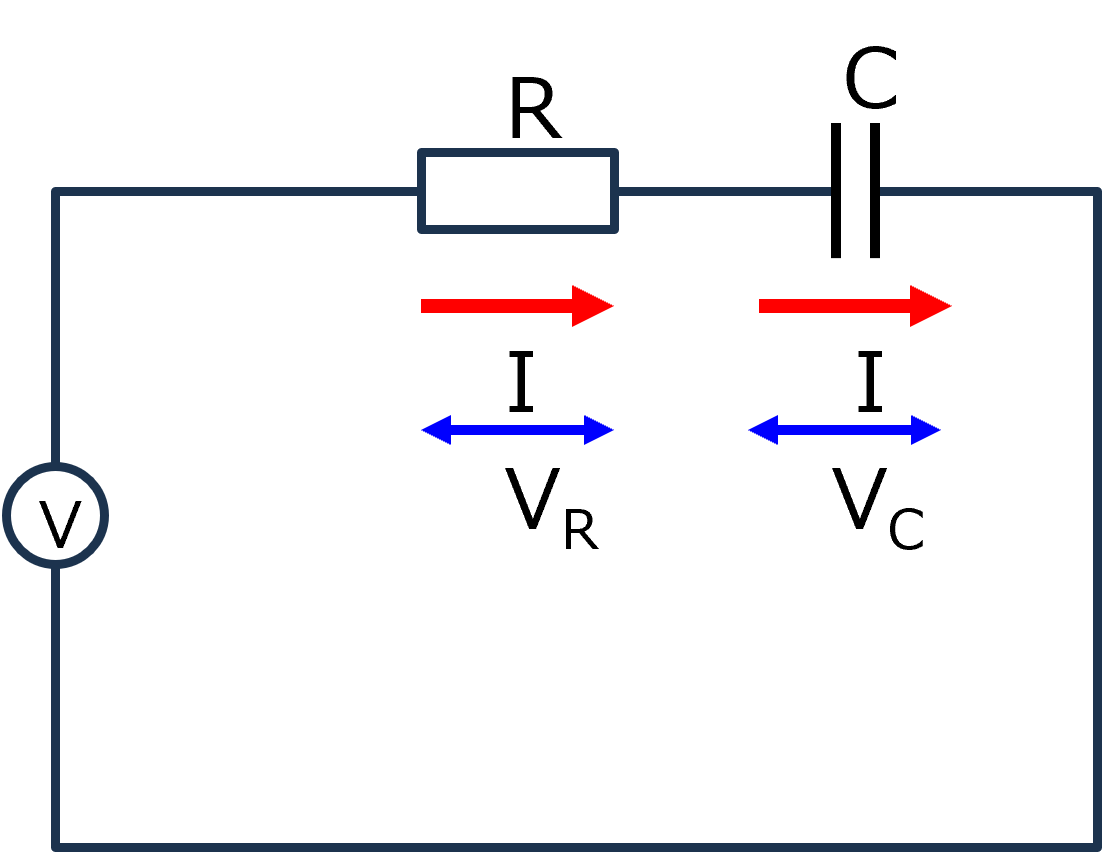
RC直列交流回路をラプラス変換で真面目に解く - 電流を主体に考える

RとCが直列に並んだ交流回路をラプラス変換でまじめに考えます．式は，

\(\Large R \cdot I(t) + \displaystyle \frac{1}{ C} \int I(t) \ dt = V_0 \cdot e^{ j \omega t} \)　

となるので，一回微分して，

\(\Large \displaystyle R \frac{d \ I(t)}{dt} + \frac{1}{ C} I(t) = j \omega \cdot V_0 \cdot e^{ j \omega t} \)　

ラプラス変換は，F(s)，とすると，

\(\Large \displaystyle \mathfrak{ L} \left[ \frac{df}{dt}\right] = sF(s)-f(0) \)

\(\Large \displaystyle \mathfrak{ L} \left[ e^{-bt}\right] = \frac{1}{s+b} \)

したがって，

\(\Large \displaystyle R \{sF(s)-I(0)\} + \frac{1}{C} \ F(s) = V_0 \cdot j \omega \ \frac{1}{s - j \omega} \)

初期条件，I(0)=0，から，

\(\Large \displaystyle R \cdot sF(s) + \frac{1}{C} \ F(s) = V_0 \cdot j \omega \ \frac{1}{s - j \omega} \)

となります．ここで，

\(\Large \displaystyle a \equiv \frac{1}{RC}\)

とおくと，

\(\Large \displaystyle sF(s) + a \ F(s) = V_0 \cdot \frac{ j \omega}{R} \frac{1}{s - j \omega}\)

\(\Large \displaystyle F(s) = V_0 \cdot \frac{ j \omega}{R} \frac{1}{s - j \omega} \frac{1}{s + a}\)

式を変形して，

\(\Large \displaystyle F(s) = \frac{A}{s - j \omega} + \frac{B}{s + a} \)

とすると，

\(\Large \displaystyle V_0 \cdot \frac{ j \omega}{R} \frac{1}{s - j \omega} \frac{1}{s + a} = \frac{A}{s - j \omega} + \frac{B}{s + a}\)

\(\Large \displaystyle =\frac{A(s+a) + B(s - j \omega)}{(s - j \omega)(s+a)}\)

\(\Large \displaystyle V_0 \cdot \frac{ j \omega}{R} = (A+B)s +Aa-j \omega B\)

右辺第一項はｓを含む項ですが左辺には存在しないので，

\(\Large \displaystyle A+B=0 \rightarrow B=-A\)

\(\Large \displaystyle \frac{ j \omega}{R} = Aa-j \omega B = A (a+j \omega) \)
\(\Large \displaystyle A = V_0 \cdot \frac{j \omega}{R (a+j \omega)} \)
\(\Large \displaystyle B = - V_0 \cdot \frac{j \omega}{R (a+j \omega)} \)
\(\Large \displaystyle F(s) = V_0 \cdot \frac{j \omega}{R (a+j \omega)} \left( \frac{1}{s - j \omega} - \frac{1}{s + a} \right) \)

逆ラプラス変換は，

\(\Large \displaystyle \mathfrak{ L^{-1}} \left[ \frac{1}{s+a}\right] = e^{-at} \)
\(\Large \displaystyle \mathfrak{ L^{-1}} \left[ \frac{1}{s- j \omega}\right] = e^{-j \omega t} \)

となるので，

\(\Large \displaystyle I(t) = V_0 \cdot \frac{j \omega}{R (a+j \omega)} \left( e^{ j \omega t} - e^{-at} \right) \)
\(\Large \displaystyle = V_0 \cdot \frac{j \omega}{\frac{1}{C}+j \omega R } \left( e^{ j \omega t} - e^{- \frac{1}{RC}t} \right) \)
\(\Large \displaystyle = V_0 \cdot \frac{j \omega C}{1+j \omega RC } \left( e^{ j \omega t} - e^{- \frac{1}{RC}t} \right) \)
\(\Large \displaystyle = V_0 \cdot \frac{j \omega C + \omega^2 R C^2}{1+ (\omega RC)^2 } \left( e^{ j \omega t} - e^{- \frac{1}{RC}t} \right) \)
\(\Large \displaystyle = V_0 \cdot \frac{ \frac{j}{\omega C} + R }{\frac{1}{ (\omega C)^2}+ R^2 } \left( e^{ j \omega t} - e^{- \frac{1}{RC}t} \right) \)

となり，一致します．

後の展開は同じですが，きちんと書くと，

\(\Large \displaystyle = V_0 \cdot \frac{R + \frac{j}{ \omega C}}{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}} \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot \left( e^{ j \omega t} - e^{- \frac{1}{ RC} t} \right) \)　

ここで，複素数の項を指数に置き換える．

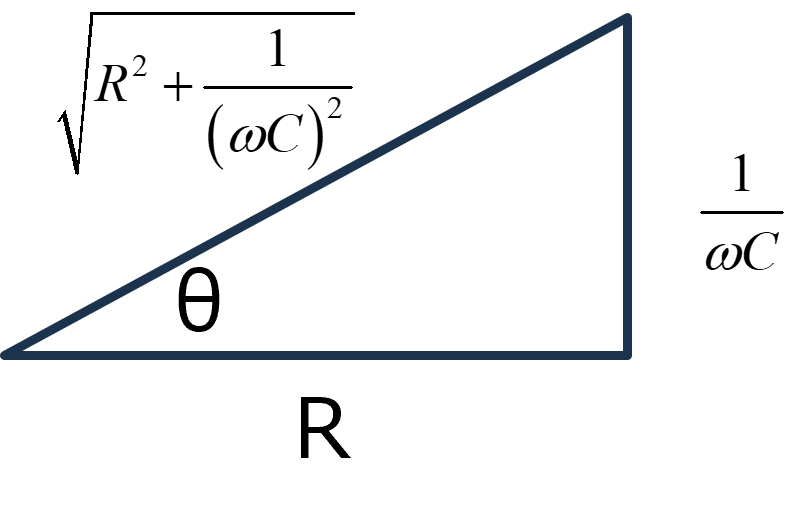
\(\Large \displaystyle cos \ \theta = \frac{R }{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}\)　

\(\Large \displaystyle j \cdot sin \ \theta = \frac{ \frac{j}{ \omega C}}{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}\)　

\(\Large \displaystyle e^{ j \ \theta} =cos \ \theta + j \cdot sin \ \theta \)　

より，

\(\Large \displaystyle \frac{R + \frac{j}{ \omega C}}{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}} = e^{ j \ \theta} \)　

ここで，

\(\Large \displaystyle tan \ \theta = \frac{1} {\omega RC} \)　

となります．したがって，

\(\Large \displaystyle I(t) = V_0 \cdot \frac{R + \frac{j}{ \omega C}}{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}} \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot \left( e^{ j \omega t} - e^{- \frac{1}{ RC} t} \right) \)

\(\Large \displaystyle = V_0 \cdot e^{ j \ \theta} \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot \left( e^{ j \omega t} - e^{- \frac{1}{ RC} t} \right)\)　

\(\Large \displaystyle = V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot \left\{ e^{ j (\omega t + \theta)} - e^{ j \ \theta} \cdot e^{- \frac{1}{ RC} t} \right\}\)　

となります．ここで，三角関数に戻すために，虚数部分のみ取り出すと，

\(\Large \displaystyle Im [ I(t) ] = Im \left[V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot e^{ j (\omega t + \theta)} \right]
- Im \left[V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot e^{ j \ \theta} \cdot e^{- \frac{1}{ RC} t} \right] \)

\(\Large \displaystyle = V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot sin (\omega t + \theta)
- V_0 \cdot \frac{1 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot sin \ \theta \cdot e^{- \frac{1}{ RC} t} \)

十分な時間が経てば，第二項は0となるので，

\(\Large \displaystyle I(t) \sim \frac{V_0 }{{ \sqrt{R^2 + \frac{1}{ (\omega C)^2 }}}} \cdot sin (\omega t + \theta) \)

\(\Large \displaystyle \theta = tan^{-1} \ \frac{1} {\omega RC} \)　

となり，インピーダンスを用いた結果と一致します．　

次は，０９－４．RC直列交流回路を真面目に解く - 電圧を主体に考える，です．