回路-05

インダクタ（コイル）

インダクタの細かい原理は置いていおいて，その性質は，

　　インダクタ，電流の時間的な変化量に比例して逆起電力が発生する

ものと考えます．式で表すと，電圧は，

\(\Large V(t) = L \displaystyle \frac{dI(t)}{dt} \)　

ここで，
　L : インダクタ　（H)
となります．電流は，

\(\Large I(t) = \displaystyle \frac{1}{L} \ \int V(t) \ dt \)　

となります．ちょうどコンデンサと逆の関係になります．

・交流電源

教科書には，電圧入力，と，電流入力，とありますが，今回はすべて，電圧入力，で考えます．交流電源（電圧）を加えた場合，

\(\Large V(t) = V_0 \ sin \ (\omega t )\)　

となりますので，電流は，

\(\Large I(t) = \displaystyle \frac{1}{L} \ \int V(t) \ dt= -\frac{ V_0}{ \omega L} \ cos \ (\omega t ) + D \)　

となります．

\(\Large sin (a-b) = sin \ a \cdot cos \ b - cos \ a \cdot sin \ b\)　

\(\Large sin (a- \frac{ \pi}{2} ) = sin \ a \cdot cos \ \frac{ \pi}{2}- cos \ a \cdot sin \ \frac{ \pi}{2} = - cos \ a \)　

から，

\(\Large I(t) = \displaystyle -\frac{ V_0}{ \omega L} \ cos \ (\omega t ) + D = \frac{ V_0}{ \omega L} \ sin \ \left(\omega t - \frac{ \pi}{2} \right) + D\)　

となるので，

初期条件は，

t=0, I(0) = 0，ですので，

\(\Large I(０) = \displaystyle -\frac{ V_0}{ \omega L} \ sin \ (\omega \cdot 0 - \frac{ \pi}{2}) + D = -\frac{ V_0}{ \omega L} + D = 0 \)　

\(\Large D = \frac{ V_0}{ \omega L} \)　

\(\Large I(t) = \displaystyle \frac{ V_0}{ \omega L} \ sin \ \left(\omega t - \frac{ \pi}{2} \right) + \frac{ V_0}{ \omega L} = \frac{ V_0}{ \omega L} \left\{ 1 + sin \ \left(\omega t - \frac{ \pi}{2} \right) \right\}\)　

となります．位相がπ/2だけシフトします．コンデンサのときとは逆のシフトとなります．さらに，電流はプラスマイナスではなく，０から，となります．　

・LTspice

実際にL交流回路を作ってみてシミュレートしてみました．

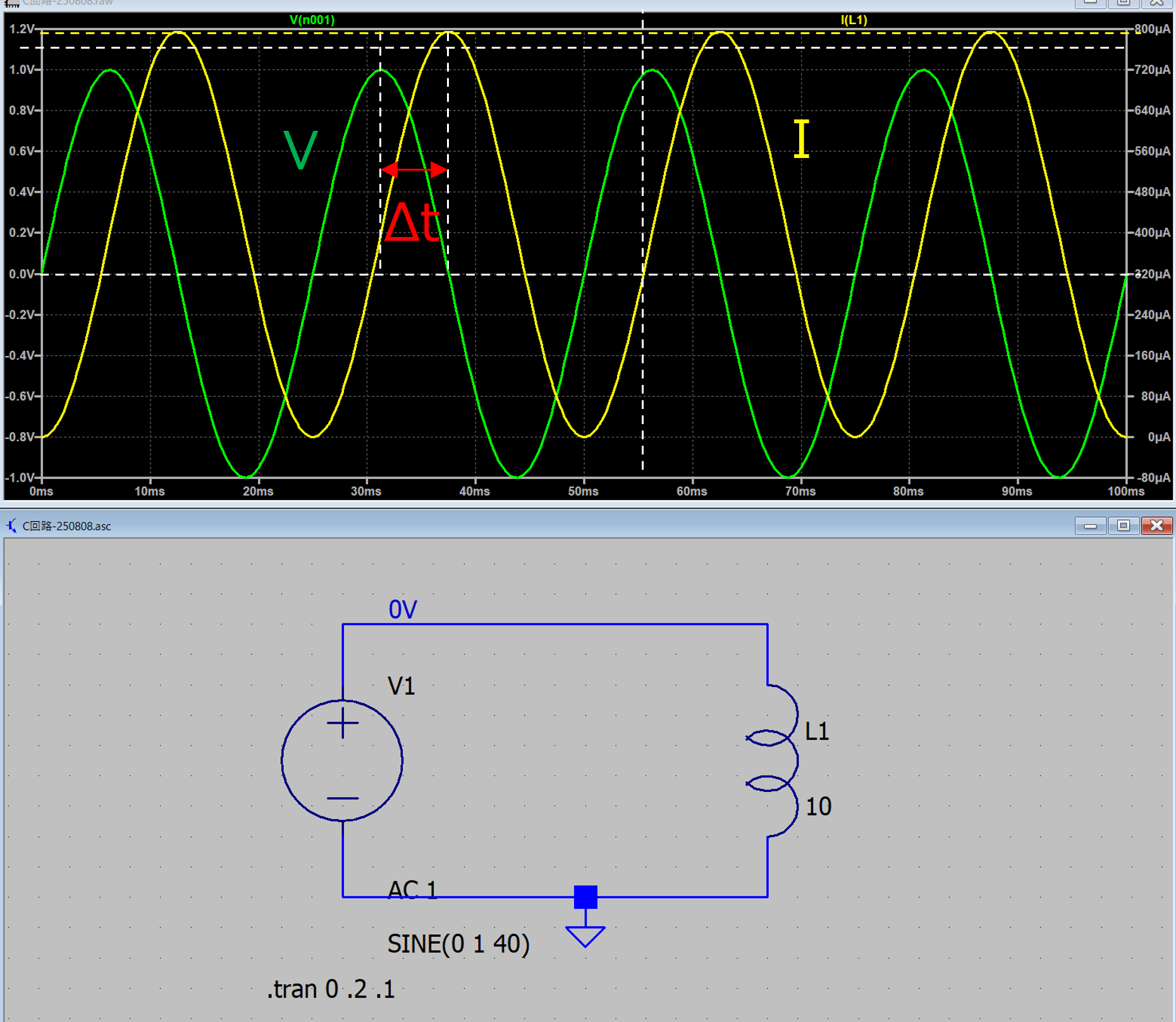
条件は，
　f = 40 Hz
　L = 10 H
　V₀ = 1 V
ということで，

\(\Large \omega = 40 \cdot 2 \cdot \pi = 251.3 \ rad/s \)　

振幅

インダクタ直下の電流値の振幅は，

\(\Large \frac{ V_0}{C \cdot \omega } = 398 \mu A \)　

と電流の振幅が計算どおりとなっていることがわかります．

位相

今回は，この計算は使わずに，頂点同士の差（電流は０を横切らないので）から求めました．

\(\Large \Delta t = 5.90 \ ms \)　

周波数は40 Hz，ですので，一周期が，1/40 = 25 ms.

\(\Large \phi= \frac{5.90}{25} \times 360 = 84 \ (degree) \)　

と若干異なりますが，約90度（π/2），ズレていることがわかります．

次ページは，指数関数表示について考えていきます．