誕生日パラドクス-06
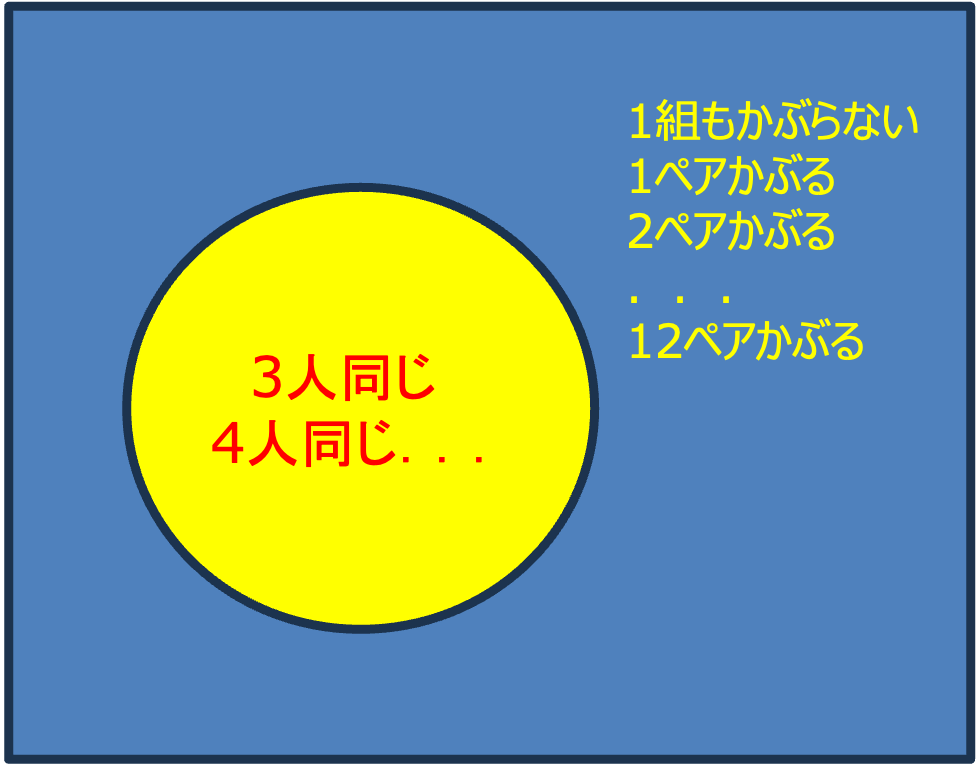
25人の中で3人が同じ,ほかはなんでもいいの場合
を集合で考えると,.

条件にあう場合 : 3人同じ,4人同じ...3人同じが2組...
など結構たくさんの場合があります.
なので,補集合を考えると,
すべてが被らない場合
2人のペアが,1~12組かぶる場合
と比較的,少ない場合で説明できそうです.
・すべてが被らない場合
以前のページでも説明したように,
一人目:どの日でもいいので,365/365=1
二人目:一人目以外なので,364/365
25人目:24人以外とかぶらない確率なので,(365-25+1)/365
この積は,
\( \Large P_{0} = \frac{365}{365} \frac{364}{365} \cdots \frac{341}{365} = \frac{1}{365^{25}} \frac{365!}{340!} = 0.4313 \)
となります.
・2人のペアが1組一致
25人から2人のペアを1組選ぶ場合の数は,
\( \Large _{25} C_{2} \)
です.
ペアの二人が同じ誕生日である確率
\( \Large \frac{1}{365} \)
です.
残り23人がばらばらである確率を合わせると,
\( \Large _{25} C_{2} \cdot \frac{1}{365} \cdot \frac{364}{365} \frac{363}{365} \cdots \frac{365-23}{365} =0.3794 \)
となります.
・2人のペアが2組一致
25人から2人のペアを2組選ぶ場合の数は,
\( \Large \displaystyle \frac{_{25} C_{2} \cdot _{23} C_{2}}{2!} \)
です(分母の階乗に注意).
ペアの二人が同じ誕生日である確率
\( \Large \frac{1}{365} \cdot \frac{1}{365} \)
です.
残り21人がばらばらである確率を合わせると,
\( \Large \displaystyle \frac{_{25} C_{2} \cdot _{23} C_{2}}{2!} \cdot \frac{1}{365} \frac{1}{365}\cdot \frac{364}{365} \frac{363}{365} \cdots \frac{365-22}{365} =0.1404 \)
となります.
したがって,
・2人のペアが i 組一致
25人から2人のペアをi組選ぶ場合の数は,
\( \Large \displaystyle \frac{_{25} C_{2} \cdot _{23} C_{2} \cdots _{25-2(i-1)} C_{2} }{i!} \)
です(分母の階乗に注意).
ペアの二人が同じ誕生日である確率
\( \Large \left( \frac{1}{365} \right)^i \)
です.
残りの人がばらばらである確率を合わせると,
\( \Large \displaystyle \frac{_{25} C_{2} \cdot _{23} C_{2} \cdots _{25-2(i-1)} C_{2} }{i!} \cdot \left( \frac{1}{365} \right)^i \cdot \frac{364}{365} \frac{363}{365} \cdots \frac{365-(24-i)}{365} \)
となります.
これらの確率を全部足して,1から引けばいいので,
\( \Large \displaystyle P = 1 - \left[ 0.4313 + \sum_{i=1}^{12} \frac{_{25} C_{2} \cdot _{23} C_{2} \cdots _{25-2(i-1)} C_{2} }{i!} \cdot \left( \frac{1}{365} \right)^i \cdot \frac{364}{365} \frac{363}{365} \cdots \frac{365-(24-i)}{365} \right] \)
\( \Large = 0.016409 \)
となりました.思った以上に,複雑な式となりました.
もっと簡略化できるかな?と思いましたが,これ以上は無理なようです.
私が間違えて計算した値, 0.01726,と結構近いですが,単なる偶然です.
各確率を図示すると,
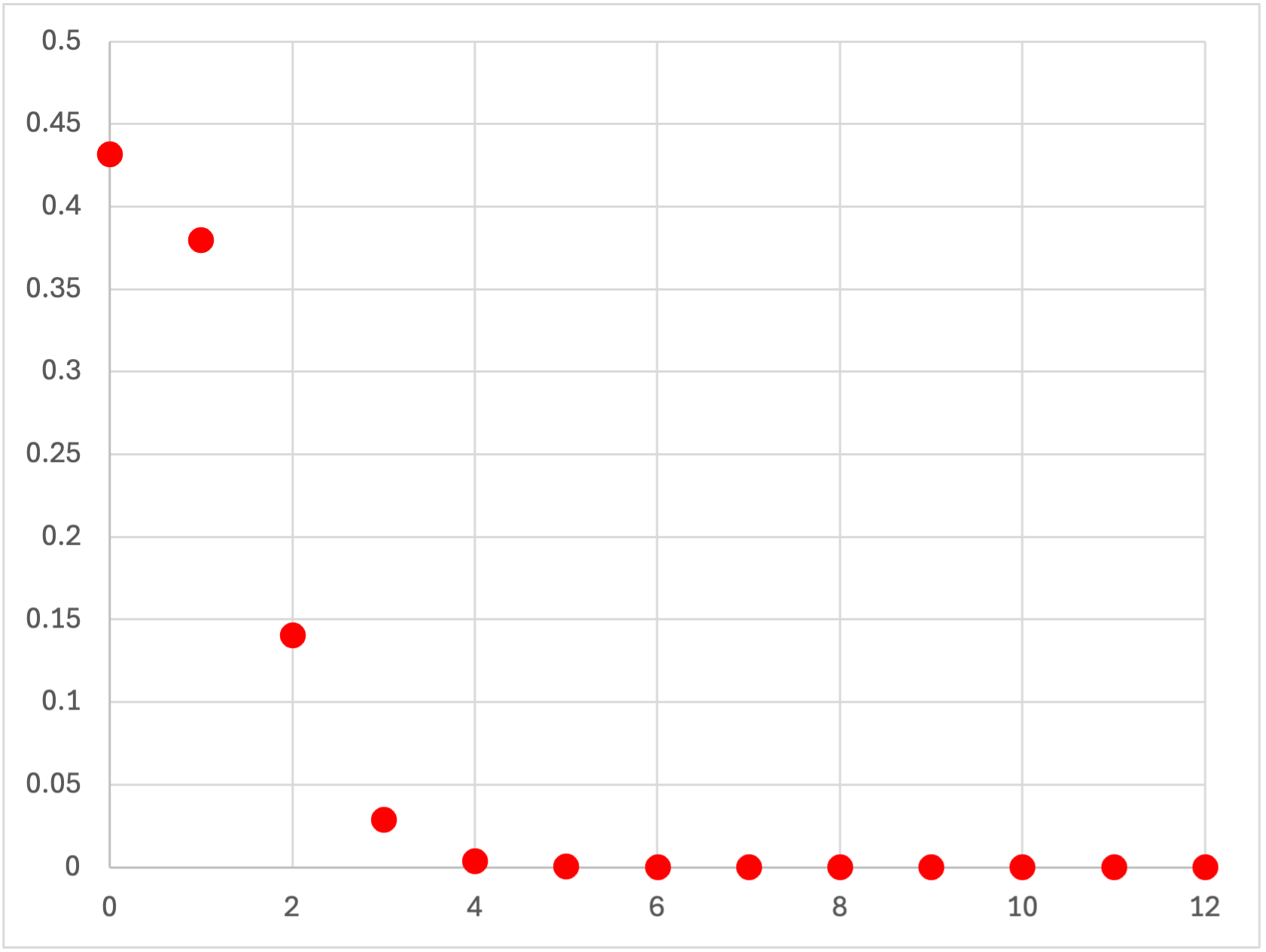
となります.縦軸を対数にすると(0を除いて)
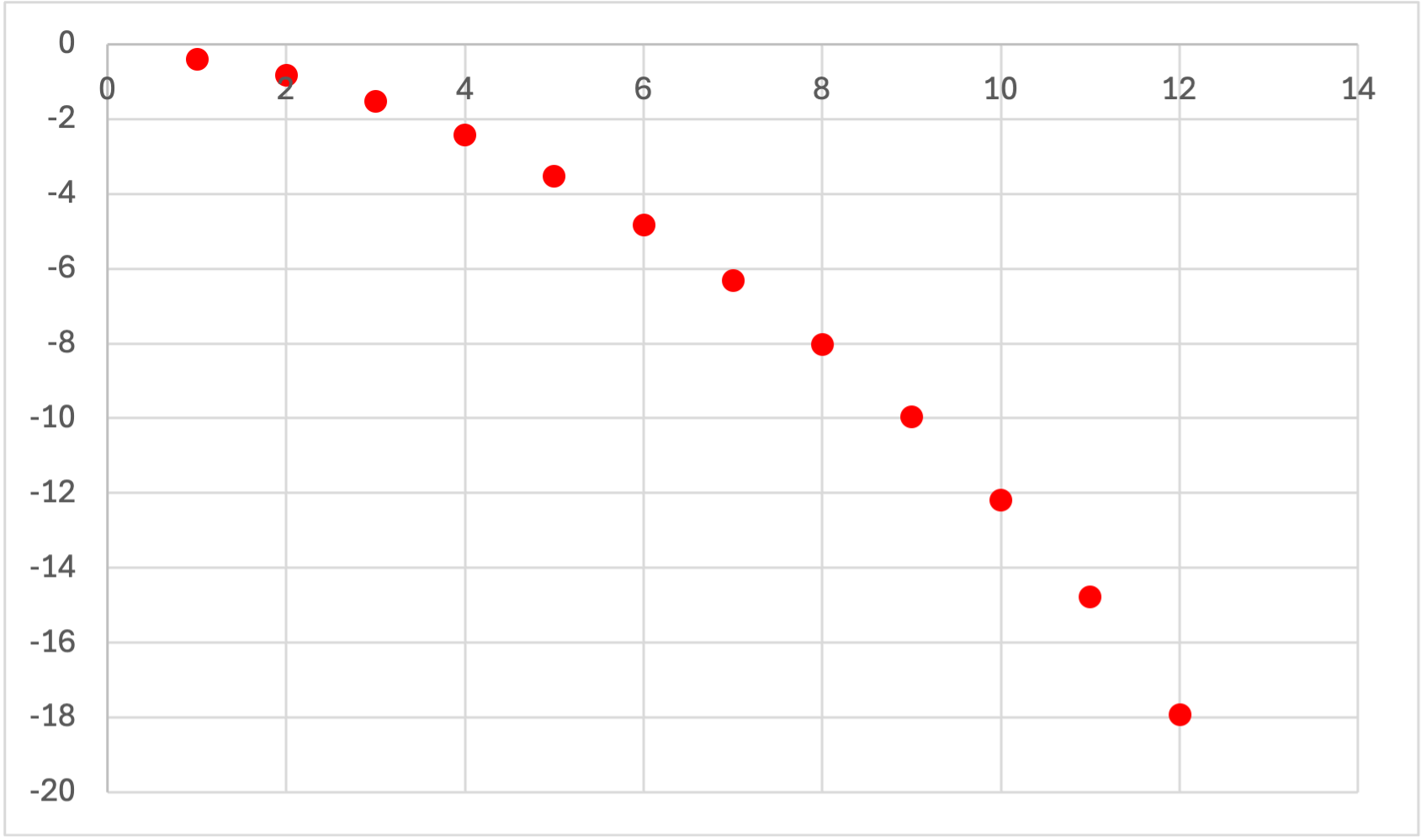
となります.
当初は,簡単な場合として提示した問題ですが,思った以上に複雑な計算式となりました.
指摘していただいた学生さん,ありがとうございます.