誕生日パラドクス-01

誕生日パラドクスという問題があります．ネットで検索しても結構なサイトで紹介されています．

今回は，この問題を講義で使いましたので，解説していきたいと思います．

前提として，
　１年は３６５日
　各人の誕生日はランダム
となります．

何人いれば誕生日が最低一組かぶるのか？

最低一組，というのはいろいろな場合が考えられます．例えば，二組とか，3人一緒とか．

しかし，補集合を考えると楽になります．

　最低一組かぶる　＝　１　ー　誰も被らない

ですので，誰も被らない確率を考えます．

一人ずつ考えていきます．

・一人目

これは，どの日でもいいので，

\( \Large p_{01} = \frac{365}{365} \)

となります．

・二人目

は，一人目の日付以外，ということになりますので，

\( \Large p_{02} = \frac{365-1}{365} = \frac{364}{365} \)

・i人目

は，i-1人の日付以外，ということになりますので，

\( \Large p_{i} = \frac{365-i+1}{365} \)

これらの確率の積が，誰も被らない確率，となるので，

\( \Large P_{i} = p_{01} \cdot p_{02} \cdots p_{i} = \frac{365}{365} \frac{364}{365} \cdots \frac{365-i+1}{365} \)

となるので，最低一組かぶる確率は，

\( \Large 1-P_{i} = \frac{365}{365} \frac{364}{365} \cdots \frac{365-i+1}{365} \)

もし，25人だとした場合は，

\( \Large 1-P_{25} = \frac{365}{365} \frac{364}{365} \cdots \frac{341}{365} = 0.5687 \)

となり，25人だとしても，誕生日がかぶる確率は半分以上となります．

思った以上に，少ない人数で50％を超えることになります．

では，何人いれば確率的に50％を超えるのでしょうか？

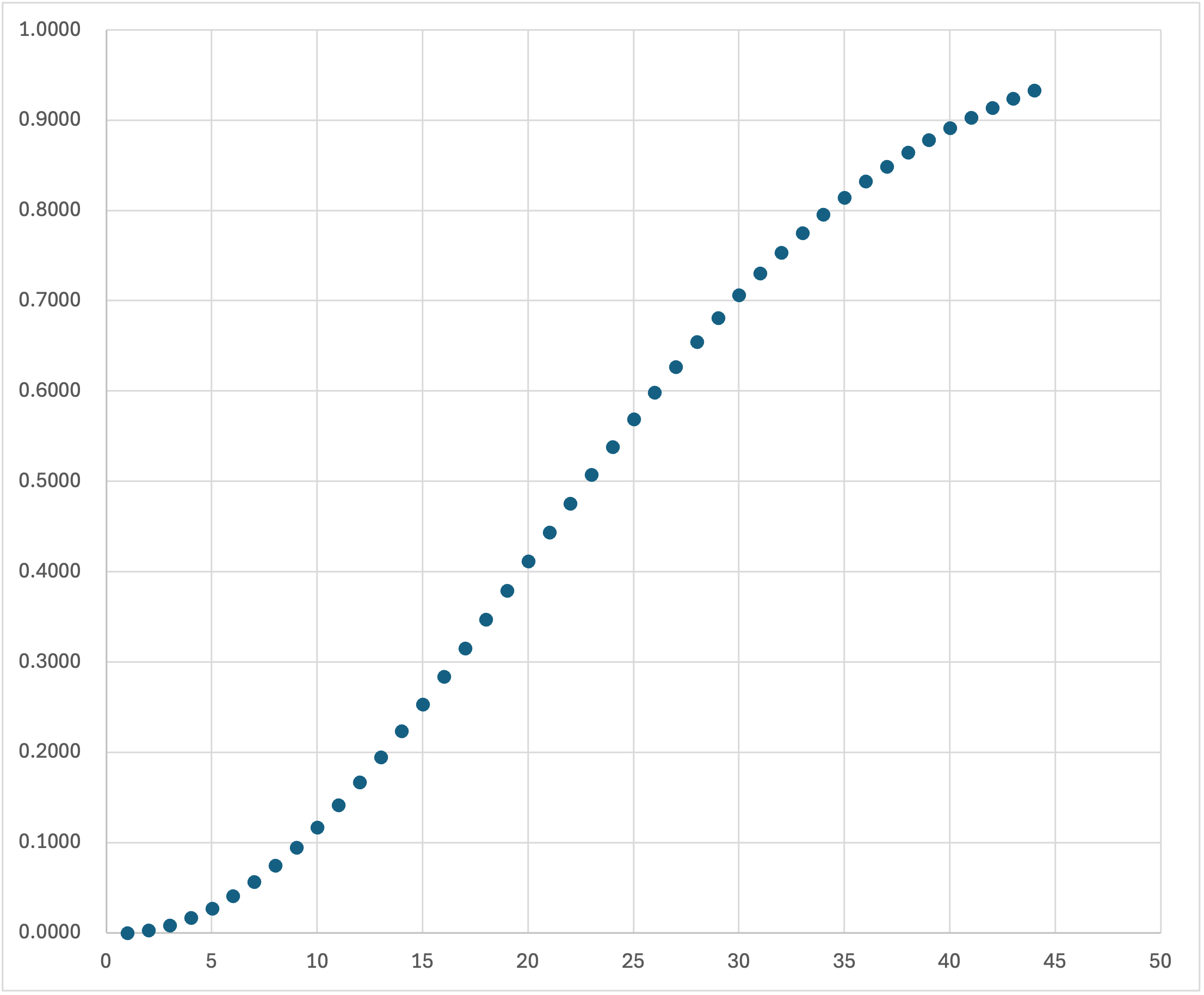
実際に計算してみると，

となり，23人の場合で50％を超えることになります．

次に，もう少し条件を厳しくした場合の確率を求めます．