Barkai-Leiblerモデルを考える-07
リカバリーフェーズでの理論・シミュレーションとの比較
各状態の時間変化は,
リカバリーフェーズでの理論とシミュレーションとの比較をおこなっていきましょう.
リカバリー速度の時定数は,
\(\Large \displaystyle k_B \cdot \frac{k_A}{k_A + k_I \cdot I} \)
となることが予想されます.
| ka | ki | kB | kR |
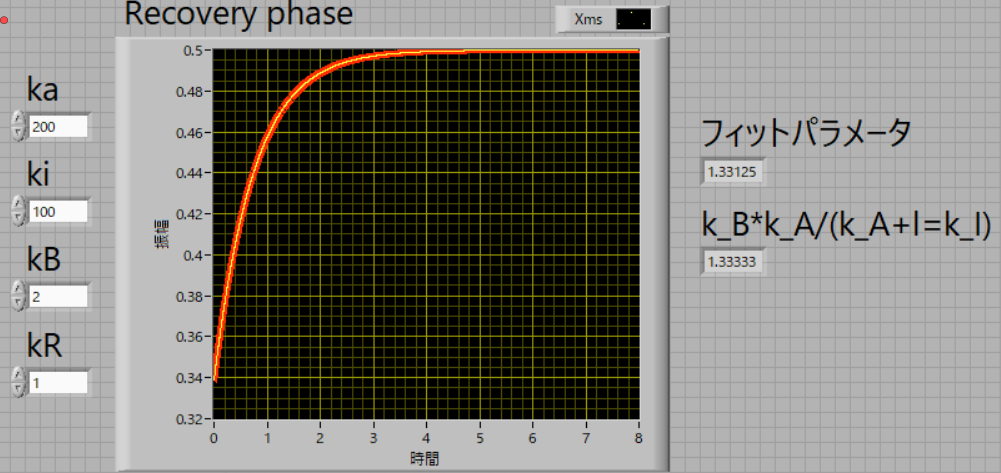
| 200 | 100 | 2 | 1 |

理論値,フィット値,1.33,で一致します.
| ka | ki | kB | kR |
| 100 | 100 | 2 | 1 |
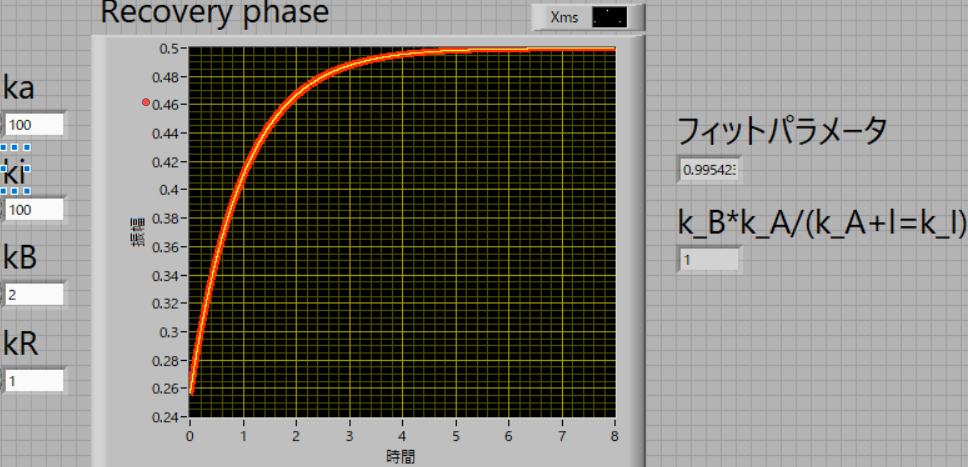
理論値,フィット値,1,で一致します.
| ka | ki | kB | kR |
| 100 | 100 | 1 | 1 |
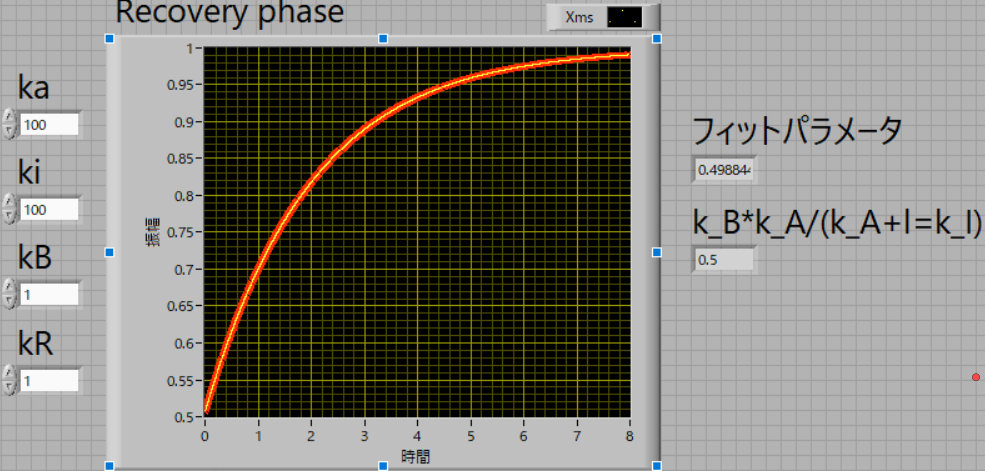
kBを変えても,理論値,フィット値,0.5,で一致します.
| ka | ki | kB | kR |
| 100 | 100 | 1 | .5 |
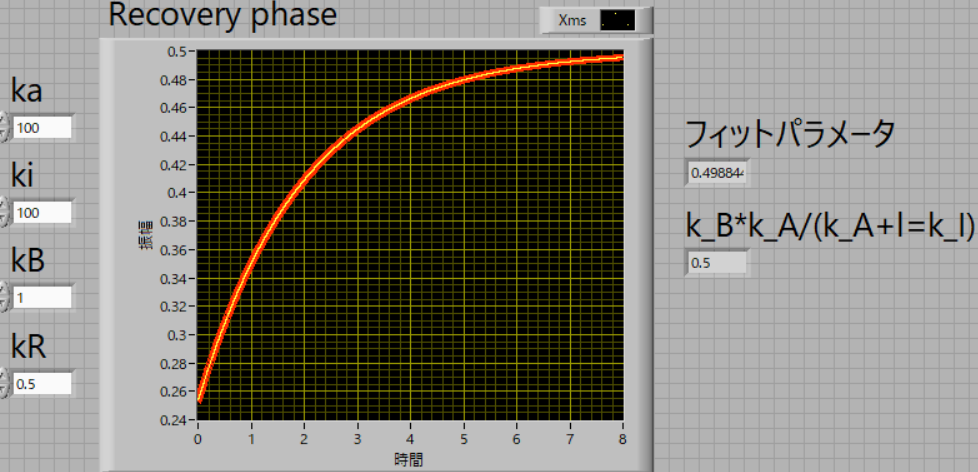
kIを変えても影響せず,理論値,フィット値,0.5,で一致します.
数学的にはいい加減でしたが,結構いい感じでフィットできています.
実際の実験結果
しかし,実際の結果は,このような指数関数ではなく,シグモイド型となります.
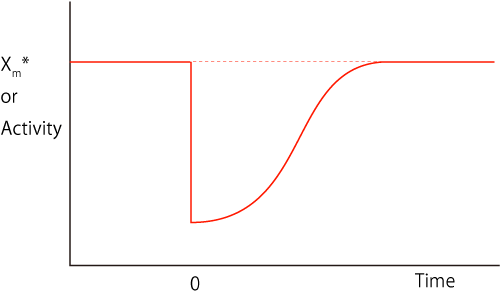
Alonの第2版にもこのようなトレースとなっています.
従って,適応現象においては何らかの協同性が関わっていることが示唆されます.