ランダム過程における自己相関関数について-03
自己相関,a=1, d=-1の場合
次に,1, -1の場合を考えます.
これは,モータの逆回転,順回転を1, -1とした場合に相当します.
前回の条件では,値を持つ場合は1通りでしたが,今回は,4通り存在します. つまり,
A→A : 1✕1 = 1
A→D : 1✕(-1) = -1
D→D : -1✕(-1) = 1
D→A : -1✕1 = -1
それぞれの場合について計算し,合計する必要があります.
・A→A
t=0, A=1に相当しますので, 先の計算と同様に,
\(\Large A_{A \rightarrow A} = P_0 + ( 1- P_0) \cdot exp \left( - \frac{t}{ \tau} \right) \)
となります.
・A→D
この場合は,A状態からは,AかDにしか遷移しないので, 1-(A→A) を計算すればよい.
\(\Large \begin{eqnarray} A_{A \rightarrow D} &=& 1 - \left[ P_0 + ( 1- P_0) \cdot exp \left( - \frac{t}{ \tau} \right) \right] \\
&=& (1 - P_0) \cdot \left[ 1 - exp \left( - \frac{t}{ \tau} \right) \right] \\
\end{eqnarray} \)
となります.
・D →A
この場合には,初期条件を,t=0, A=0として計算すればよいので,
\(\Large A = P_0 + D \cdot exp \left( - \frac{t}{ \tau} \right) \)
\(\Large 0 = P_0 + D \)
\(\Large D = - P_0 \)
\(\Large A_{D \rightarrow A} = P_0 \cdot \left[ 1 - exp \left( \frac{t}{ \tau} \right) \right] \)
となる.
・D →D
A→D,の場合と同様に,1-(D→A) を計算すればよい.
\(\Large A_{D \rightarrow D} = 1 - P_0 \cdot \left[ 1 - exp \left( \frac{t}{ \tau} \right) \right] \)
自己相関関数,それぞれの場合に以下の係数を掛ければよい.
| 係数 | f(t) | |
| A→A | 1 | P0 |
| A→D | -1 | P0 |
| D→A | -1 | 1-P0 |
| D→D | 1 | 1-P0 |
\(\Large A_{A \rightarrow A} : P_0 \left[P_0 + ( 1- P_0) \cdot exp \left( - \frac{t}{ \tau} \right) \right] = P_0^2 + P_0 \cdot ( 1- P_0) \cdot exp \left( - \frac{t}{ \tau} \right)\)
\(\Large A_{A \rightarrow D} : - P_0 \cdot (1-P_0) \cdot \left[ 1 - exp \left( - \frac{t}{ \tau} \right) \right] = - P_0 \cdot (1-P_0) + P_0 \cdot ( 1- P_0) \cdot exp \left( - \frac{t}{ \tau} \right) \)
\(\Large A_{D \rightarrow A} :-( 1 - P_0) \cdot P_0 \cdot \left[ 1 - exp \left( \frac{t}{ \tau} \right) \right] = - P_0 \cdot (1-P_0) + P_0 \cdot ( 1- P_0) \cdot exp \left( - \frac{t}{ \tau} \right) \)
\(\Large A_{D \rightarrow D} : ( 1 - P_0) \cdot \left[ 1 - P_0 \cdot \left( 1 - exp \left( \frac{t}{ \tau} \right) \right) \right] = (1-P_0)^2 + P_0 \cdot ( 1- P_0) \cdot exp \left( - \frac{t}{ \tau} \right) \)
ここで,指数がかかっていない項の合計は,
\(\Large P_0^2 -2 \cdot P_0 \cdot ( 1 - P_0 ) + ( 1 - P_0 )^2 = (2 \cdot P_0 - 1 )^2 \)
と簡略化できます. 指数がかかっている項はすべて同じなので,結果,
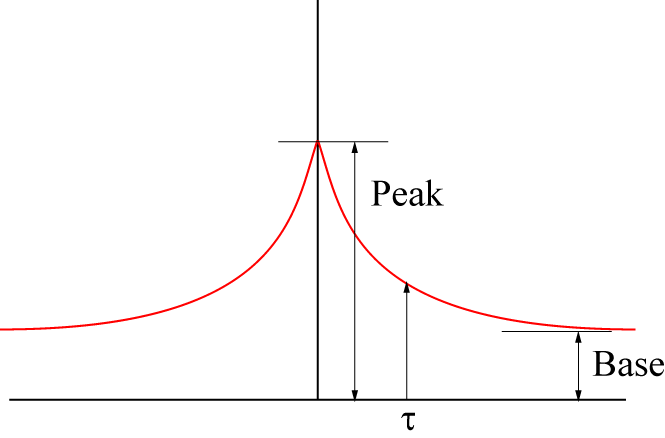
\(\Large <f(t) f(t+ \tau)> = (2 \cdot P_0 - 1 )^2 + 4 \cdot P_0 \cdot ( 1- P_0) \cdot exp \left( - \frac{t}{ \tau} \right) \)
となります.つまり,

\(\Large Peak : \hspace{ 18pt } ( 2 \cdot P_0 - 1 )^2+ 4 \cdot P_0 \cdot ( 1- P_0) = 1 \)
\(\Large Base : \hspace{ 18pt } ( 2 \cdot P_0 - 1 )^2 \)
\(\Large \tau : \hspace{ 18pt } \frac{1}{k_{+} + k_{-}} \)
つまり,t=0においては必ず1となります.
もし,
k+ = k-
の場合,P0 = 0.5,となります.また,
\(\Large <f(t) f(t+ \tau)> = (2 \cdot P_0 - 1 )^2 + 4 \cdot P_0 \cdot ( 1- P_0) \cdot exp \left( - \frac{t}{ \tau} \right) \)
の第一項が0となります.
\(\Large \tau = 4 \cdot k_- = \frac{4}{3} \cdot k_+ \)
\(\Large t=0 \hspace{ 18pt } <f(t) f(t+ \tau)>=1 \)
\(\Large t= \infty \hspace{ 18pt } <f(t) f(t+ \tau)>=0 \)
となります.
もし,
k+ = 3k-
の場合,P0 = 0.75,となります.
\(\Large t=0 \hspace{ 18pt } <f(t) f(t+ \tau)>=1 \)
\(\Large t= \infty \hspace{ 18pt } <f(t) f(t+ \tau)>=0.25 \)
となります.
次ページに,A状態(値a)とD状態(値d)のa, d, の一般解を計算してみましょう.