ふりこ-05

エネルギー保存則

ふりこの運動には運動エネルギーと位置エネルギーが関わってきています．

摩擦などの減衰がなければ，ずーっと振動し続けています．

その際のエネルギーは保存されているはずですが，確かめてみましょう（ここ，を参考にしました）．

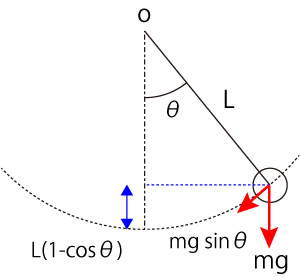
図のように，振り子の位置（θ）によって運動エネルギーと位置エネルギーの値，割合は異なります．

もちろん，
　 θが最大値の時に，速度０，位置エネルギー最大
　θが０の時に，速度最大，位置エネルギー最低
となりますね．

まずは，原点をふりこの回転の中心，o，とします．

ここ，に記載したように，運動方程式は，

\( \Large F = m \ \alpha = - m \ g \ sin \theta \)

となりますね．

\(\Large \alpha = \frac{d \upsilon}{dt} \)

\(\Large \upsilon = L \frac{d \theta}{dt} \)

なので，運動方程式を両辺に速度をかけて，書き換えると

\( \Large m \ \upsilon \frac{d \upsilon}{dt} = - m \ g \ L \ sin \theta \ \frac{d \theta}{dt} \)

時刻，t₀からｔ，まで積分すると，

\( \Large \displaystyle \int_{t_0}^{t} m \ \upsilon \frac{d \upsilon}{dt} dt = \displaystyle \int_{t_0}^{t} - m \ g \ L \ sin \theta \ \frac{d \theta}{dt} \ dt \)

置換積分を行い，積分範囲を変更します．

t₀ -> t

v(t₀) -> v(t)

θ(t₀) -> θ(t)

となるので，

\( \Large m \displaystyle \int_{\upsilon (t_0)}^{\upsilon(t)} \upsilon \ d \upsilon = - m \ g \ L \displaystyle \int_{\theta (t_0)}^{\theta (t)} \ sin \theta \ d \theta \)

となります．この積分は簡単で，左辺は，

\( \Large m \left[ \frac{1}{2} \upsilon^2 \right]_{\upsilon(t_0)}^{\upsilon(t)} = \frac{1}{2} m \upsilon(t)^2 -\frac{1}{2} m \upsilon(t_0)^2 \)

となり，右辺は，

\( \Large - m \ g \ L \left[ - cos \theta \right]_{\theta(t_0)}^{\theta (t)} = m \ g \ L \ cos \theta(t_0) - m \ g \ L \ cos \theta(t) \)

まとめると，

\( \Large = \frac{1}{2} m \upsilon(t_0)^2 -m \ g \ L \ cos \theta(t_0) = \frac{1}{2} m \upsilon(t)^2 -m \ g \ L \ cos \theta(t) \)

ここで，原点を回転の中心から，振り子の最下点に変更します．

{x, y} -> {x, y+L}

となるので（Lを足す），上記の式は，

\( \Large \frac{1}{2} m \upsilon(t_0)^2 +m \ g \ L (1- \ cos \theta(t_0)) = \frac{1}{2} m \upsilon(t)^2 +m \ g \ L (1- \ cos \theta(t) )\)

最下点では，θ=0，なので，

\( \Large \frac{1}{2} m \upsilon_0^2 = \frac{1}{2} m \upsilon(t)^2 +m \ g \ L (1- \ cos \theta(t) )\)

\( \Large L (1- \ cos \theta(t) )\)　は，最下点からの高さを示しますので，

\( \Large m \ g \ L (1- \ cos \theta(t) )\)　は位置エネルギーとなります．

つまり，速度エネルギーと位置エネルギーとの総和は常に一定　＝　エネルギーが保存している，ということになるのです．